Question

A thin glass rod is bent into a semicircular shape of radius R. A charge +Q is uniformly distributed along the upper half and a charge −Q is distributed uniformly along the lower half as shown. The electric field at the centre P is:

Answer 1

Charge is uniformly distributed over the semicircular structure. But in the top portion positive charge is distributed and in the bottom half the negative charge is distributed. We use coulomb's law to find the electric field at the center due to small strips and we integrate over the entire structure.

Formula used:
$E = \dfrac{{kq}}{{{r^2}}}$

Complete step by step answer:
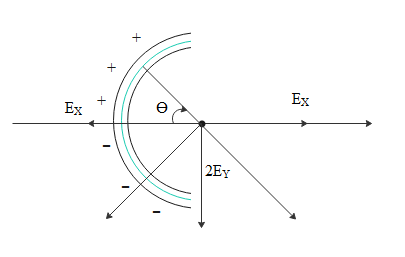
We were given with a semicircular continuous distribution of charge. We will find the electric field magnitude and direction at center due to small strips which will be symmetrical in the upper half and the lower half. For clear understanding the diagram representing the resultant electric field is given below.

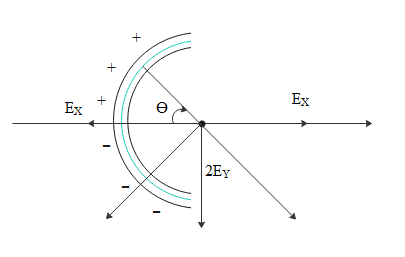
Due to the small element in the top half the electric field will be in the 4th quadrant. Due to a similar asymmetrical small element in the lower half, the electric field will be towards it as it is negatively charged i.e. towards the 3rd quadrant.
Magnitudes of fields will be the same. Hence their x components will get cancelled and only y components will get added up in the negative y direction. We will find out using coulomb's law.
The equation is
$E = \dfrac{{kq}}{{{r^2}}}$
Due to small charge the field will be
$dE = \dfrac{{kdq}}{{{r^2}}}$
At the center of that semicircular ring, horizontal components of the electric fields due to the top half and bottom half will get cancelled out as the structure is symmetrical about the x- axis and only y components will be added up.
We will find the y component of the electric field at the center due to one half first and then multiply it with number 2 to get the electric field at the center due to the total semi circular ring.
We will convert the small charge dq in terms of theta to continue the integration. Charge dq will be the product of linear charge density $\dfrac{Q}{{\left( {\dfrac{{\pi r}}{2}} \right)}}$ and length of that small element $rd\theta$ where ‘r’ is the radius and $\theta$ is the angle made by that element electric field with x axis.
Now we will apply the formula and find out the field in the following steps.
\eqalign{ & d{E_{res}} = 2dE\sin \theta = 2\dfrac{{kdq}}{{{r^2}}}\sin \theta \cr & \Rightarrow d{E_{res}} = 2\dfrac{{k\left( {\dfrac{Q}{{\left( {\dfrac{{\pi r}}{2}} \right)}}rd\theta } \right)}}{{{r^2}}}\sin \theta \cr & \Rightarrow d{E_{res}} = \dfrac{{4kQ}}{{\pi {r^2}}}\sin \theta d\theta \cr & \Rightarrow \int\limits_0^E {d{E_{res}}} = \int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{4kQ}}{{\pi {r^2}}}\sin \theta d\theta } \cr & \Rightarrow E = \dfrac{{4kQ}}{{\pi {r^2}}}\left[ { - \cos \theta } \right]_0^{\dfrac{\pi }{2}} \cr & \Rightarrow E = \dfrac{{4kQ}}{{\pi {r^2}}}\left[ {\cos (0) - \cos (\dfrac{\pi }{2})} \right] \cr & \Rightarrow E = \dfrac{{4kQ}}{{\pi {r^2}}} \cr & \Rightarrow E = \dfrac{{4Q}}{{\left( {4\pi {\varepsilon _0}} \right)\pi {r^2}}} \cr & \therefore E = \dfrac{Q}{{{\pi ^2}{\varepsilon _0}{r^2}}} \cr}
Hence field at center will be $E = \dfrac{Q}{{{\pi ^2}{\varepsilon _0}{r^2}}}$ and directed in downward i.e in negative y direction.

Note:
Since the charged distribution is uniform and opposite in sign, the x components of the semi circular structure got cancelled and only y components got added up. If the charge distribution is of the same sign then the y components will get cancelled and x components will add up. For a complete ring of the same charge distribution, the field at center will be zero.