Question

A thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is:

$\text{A}\text{. }IBL$
$\text{B}\text{. }\dfrac{IBL}{\pi }$
$\text{C}\text{. }\dfrac{IBL}{2\pi }$
$\text{D}\text{. }\dfrac{IBL}{4\pi }$

Answer 1

Consider a small arc of the circular loop. Find the net horizontal and the net vertical tension acting on this arc. Then find the magnetic force exerted on this arc. Since the loop is in equilibrium, net force on the loop must be zero.
Formula used:
$\overrightarrow{F}=I\left( \overrightarrow{L}\times \overrightarrow{B} \right)$

Complete answer:
Let the tension in the wire be T. Consider a small portion of the circular wire (radius R), which subtends a small angle $\theta$ at the centre of the circle as shown in the figure.

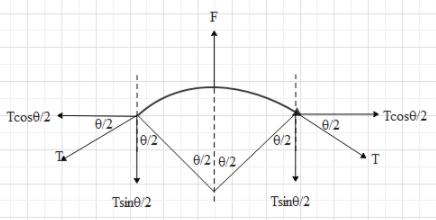
The tension at both then ends of the section, will be pulling the string downwards.
Resolve the tension into its horizontal and vertical components as shown. The horizontal component is $T\cos \dfrac{\theta }{2}$ and the vertical component is $T\sin \dfrac{\theta }{2}$.
Since the two horizontal forces are equal in magnitude but opposite in direction, the net horizontal force is zero.
The net vertical tension will be $T\sin \dfrac{\theta }{2}+T\sin \dfrac{\theta }{2}=2T\sin \dfrac{\theta }{2}$ acting downwards.
The magnetic force exerted on a straight current carrying wire is given as $\overrightarrow{F}=I\left( \overrightarrow{L}\times \overrightarrow{B} \right)$, where $\overrightarrow{L}$ is the length vector of the wire and its direction is along the direction of the current.
In this case, since the arc is very small, we can consider it as straight wire. Form arc length formula, the length of the arc is $l=R\theta$. And the direction of $\overrightarrow{L}$ will be a horizontal point towards the positive x-axis.
Therefore, the magnitude of $\overrightarrow{F}=I\left( \overrightarrow{L}\times \overrightarrow{B} \right)$ will be $F=IlB=IR\theta B$ and its direction will be upwards.
Therefore, the magnetic force will be pulling the wire section upwards.
Since the wire is in equilibrium, the upward force will be equal to the downward force.
i.e. $2T\sin \dfrac{\theta }{2}=IR\theta B$.
For small angles, $\sin \dfrac{\theta }{2}\approx \dfrac{\theta }{2}$
$\Rightarrow 2T\dfrac{\theta }{2}=IR\theta B$
$\Rightarrow T=IRB$ …. (i)
The circumference (total length) of the wire is $L=2\pi R$.
$\Rightarrow R=\dfrac{L}{2\pi }$
Substitute the value of R in (i).
$\Rightarrow T=\dfrac{ILB}{2\pi }$

Hence, the correct option is C.

Note:
Note that the approximation $\sin \dfrac{\theta }{2}\approx \dfrac{\theta }{2}$ for small angles, is valid only when the angle is measured in radians. That means $\theta$ must be in radians and not in degrees. Here, the angle must be less than 5 degrees.