Question

A thin equiconvex lens of glass of refractive index $1.5$ with radius of curvature $R$ is placed on a horizontal plane mirror. When between the lens and mirror is filled with a liquid, an object held at a distance $D$ vertically above the lens is found to coincide with its own image. The refractive index of the liquid is
(A) $2 + \dfrac{D}{R}$
(B) $2 - \dfrac{D}{R}$
(C) $2 - \dfrac{R}{D}$
(D) $2 + \dfrac{R}{D}$

Answer 1

Hint To solve this question, we need to find the equivalent focal length of the whole lens system using the lens maker’s formula. Then, using the conditions given in the question, we can determine the value of the refractive index of the liquid.

Formula Used: In this solution we will be using the following formula,
$\dfrac{1}{f} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
where $f$ is the focal length of the combination, $\mu$ is the refractive index, ${R_1},{R_2}$ are the radii of curvatures.

Complete step by step answer
Let us represent the situation given in the question by the following figure.

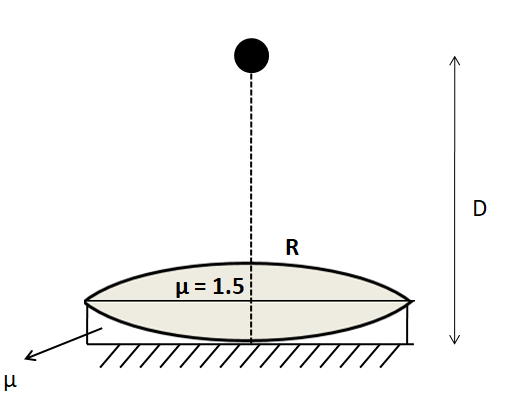
The liquid, which is present in the region between the equiconvex lens and the plane mirror, acts as a lens. So both the equiconvex lens and the liquid together form a lens system. Let the focal length of this combination be $f$ . We know that if an object is placed at the centre of the lens, then the image is produced at the centre on the other side. As the image and the object are coinciding, so distances from this combination of the lenses must be equal. So, both the image and the object must be placed at the centre of the lens combination. Since the object distance from the combination is given to be $D$ , so we have
$2f = D$
$\Rightarrow f = \dfrac{D}{2}$ (1)
Now, the focal length of the equiconvex lens is given by the lens maker’s formula as
$\dfrac{1}{{{f_1}}} = \left( {1.5 - 1} \right)\left( {\dfrac{1}{R} - \dfrac{1}{{ - R}}} \right)$
$\Rightarrow \dfrac{1}{{{f_1}}} = 0.5\left( {\dfrac{2}{R}} \right)$
On taking the reciprocal we get
${f_1} = R$ (2)
Also, the focal length of the liquid as a lens is given by
$\dfrac{1}{{{f_2}}} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{ - R}} - \dfrac{1}{\infty }} \right)$ (radius of the plane surface is infinity)
$\Rightarrow \dfrac{1}{{{f_2}}} = - \dfrac{{\left( {\mu - 1} \right)}}{R}$
Taking the reciprocal, we get
${f_2} = - \dfrac{R}{{\left( {\mu - 1} \right)}}$ (3)
By the combination of thin lenses, we have
$\dfrac{1}{f} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}}$
From (1), (2) and (3) we get
$\dfrac{1}{D} = \dfrac{1}{R} - \dfrac{{\left( {\mu - 1} \right)}}{R}$
$\Rightarrow \dfrac{1}{D} = \dfrac{{\left( {2 - \mu } \right)}}{R}$
Multiplying both sides by $R$ , we get
$\left( {2 - \mu } \right) = \dfrac{R}{D}$
Finally, on rearranging the terms we get
$\mu = 2 - \dfrac{R}{D}$
Hence, the correct answer is option C.

Note
We need to take care to consider the sign convention for the radius of curvatures of the surfaces of a lens before putting them into the Lens maker’s formula. We need to consider a particular direction as positive and then take the opposite direction as negative.