Question

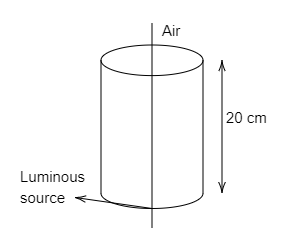
A thin equiconvex glass lens ${\mu _g} = 1.5$ is being placed on the top of a vessel of height $h = 20\,cm$ as shown in fig. A luminous point source is being placed at the bottom of the vessel on the principal axis of the lens. When the air is on both sides of the lens the image of the luminous source is formed at a distance of $20\,cm$ from the lens outside the vessel. When the air inside the vessel is being replaced by a liquid of refractive index ${\mu _1}$, the image of the same source is being formed at a distance $30\,cm$ from the lens outside the vessel. If ${\mu _1}$ is approximately $\dfrac{x}{{100}}$. Find $x$?

Answer 1

The value of the $x$ can be determined by using the formula of the thin lens equation or the lens makers formula. And by equating the lens maker formula with the focal length formula, the radius of the curvature is determined. By using this radius of the curvature and using this radius of curvature value, the ${\mu _1}$ is determined.

Formula used:
The focal length of the lens is given by,
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Where, $f$ is the focal length of the lens, $v$ is the distance of the image from the lens and $u$ is the distance of the object from the lens.
The lens maker formula is given by,
$\dfrac{1}{f} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
Where, $f$ is the focal length of the lens, $\mu$ is the refractive index of the glass, ${R_1}$ and ${R_2}$ are the radius of the curvature.

Complete step by step solution:
Given that,
The refractive index of the glass is, ${\mu _g} = 1.5$,
The height of the vessel or distance of the object is, $h = u = 20\,cm$,
The distance of the image formed is, $v = 20\,cm$,
After some changes, the distance of the image formed is, $v = 30\,cm$.
Now,
The focal length of the lens is given by,
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}\,......................\left( 1 \right)$
The lens maker formula is given by,
$\dfrac{1}{f} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)\,................\left( 2 \right)$
By equating the equation (1) and equation (2), then
$\dfrac{1}{v} - \dfrac{1}{u} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)\,................\left( 3 \right)$
By substituting the refractive index of the glass, the distance of the object and the distance of the image formed in the above equation, then
$\dfrac{1}{{20}} - \dfrac{1}{{ - 20}} = \left( {1.5 - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$
Assume that the ${R_1}$ and ${R_2}$ are equal to $R$, then
$\dfrac{1}{{20}} - \dfrac{1}{{ - 20}} = \left( {1.5 - 1} \right)\left( {\dfrac{1}{R} - \dfrac{1}{{ - R}}} \right)$
On further simplification in the above equation, then
$\dfrac{1}{{20}} + \dfrac{1}{{20}} = \left( {1.5 - 1} \right)\left( {\dfrac{1}{R} + \dfrac{1}{R}} \right)$
By adding the terms in the above equation, then
$\dfrac{2}{{20}} = 0.5 \times \dfrac{2}{R}$
On further simplification in the above equation, then
$\dfrac{1}{{10}} = \dfrac{1}{R}$
By taking reciprocal in the above equation, then the above equation is written as,
$R = 10\,cm$
For the second case, when the vessel is being filled with the liquid, then the equation (3) is written as,
$\dfrac{{{\mu _{air}}}}{v} - \dfrac{{{\mu _1}}}{u} = \left( {\dfrac{{{\mu _g} - {\mu _1}}}{{{R_1}}} - \dfrac{{{\mu _{air}} - {\mu _g}}}{{{R_2}}}} \right)\,................\left( 4 \right)$
Assume that the ${R_1}$ and ${R_2}$ are equal to $R$, then
$\dfrac{{{\mu _{air}}}}{v} - \dfrac{{{\mu _1}}}{{ - u}} = \left( {\dfrac{{{\mu _g} - {\mu _1}}}{R} + \dfrac{{{\mu _{air}} - {\mu _g}}}{{ - R}}} \right)$
On further simplification in the above equation, then
$\dfrac{{{\mu _{air}}}}{v} + \dfrac{{{\mu _1}}}{u} = \left( {\dfrac{{{\mu _g} - {\mu _1}}}{R} - \dfrac{{{\mu _{air}} - {\mu _g}}}{R}} \right)$
By substituting the ${\mu _{air}}$, ${\mu _g}$, $v$, $u$ and $R$ values in the above equation, then
$\dfrac{1}{{30}} + \dfrac{{{\mu _1}}}{{20}} = \left( {\dfrac{{1.5 - {\mu _1}}}{{10}} - \dfrac{{1 - 1.5}}{{10}}} \right)$
On further simplification in the above equation, then
$\dfrac{1}{{30}} + \dfrac{{{\mu _1}}}{{20}} = \dfrac{{1.5}}{{10}} - \dfrac{{{\mu _1}}}{{10}} + \dfrac{{0.5}}{{10}}$
By rearranging the terms in the above equation, then
$\dfrac{{{\mu _1}}}{{20}} + \dfrac{{{\mu _1}}}{{10}} = \dfrac{{1.5}}{{10}} + \dfrac{{0.5}}{{10}} - \dfrac{1}{{30}}$
On further simplification in the above equation, then
$\dfrac{{30{\mu _1}}}{{200}} = \dfrac{2}{{10}} - \dfrac{1}{{30}}$
By cancelling the terms in the above equation, then
$\dfrac{{3{\mu _1}}}{{20}} = \dfrac{2}{{10}} - \dfrac{1}{{30}}$
By cross multiplying the terms in the above equation, then
$\dfrac{{3{\mu _1}}}{{20}} = \dfrac{{60 - 10}}{{300}}$
On further simplification in the above equation, then
$\dfrac{{3{\mu _1}}}{{20}} = \dfrac{{50}}{{300}}$
By cancelling the terms in the above equation, then
$\dfrac{{3{\mu _1}}}{{20}} = \dfrac{1}{6}$
By cross multiplying the terms in the above equation, then
${\mu _1} = \dfrac{{20}}{{18}}$
By cancelling the terms in the above equation, then
${\mu _1} = 1.11$
From the equation given in the question,
${\mu _1} = \dfrac{x}{{100}}$
By equating the terms, then
$1.11 = \dfrac{x}{{100}}$

From the above equation, the value of the $x$ is $111$.

Note: The values of the, $v$ the distance of the image from the lens is given as two values, the value of the , $v$ the distance of the image from the lens is given as $20\,cm$ in the first condition, then some changes are made in the construction, then the value of the, $v$ the distance of the image from the lens is given as $30\,cm$.