Question

A thin disc of mass $M$ and radius $R$ has per unit area $\sigma(r)=kr^{2}$ where $r$ is the distance from its centre. Its momentum of inertia about an axis going through its centre of mass and perpendicular to its plane is:

& A.2\frac{M{{R}^{2}}}{6} \\\ & B.2\frac{M{{R}^{2}}}{3} \\\ & C.2\frac{2M{{R}^{2}}}{3} \\\ & D.2\frac{M{{R}^{2}}}{2} \\\ & \\\ \end{aligned}$$

Answer 1

Moment of inertia is the property of a body to resist angular acceleration. It is also the sum of the product of the masses of every particle with the square of the distances from the chosen axis of rotation. It is also known as the angular mass or rotational inertia.
Formula used:
$I=mr^{2}$

Complete answer:
The general formula of the moment of inertia is given by,$I=mr^{2}$ where, $m$is the sum of the masses of the body, and $r$ is the distance from the axis of rotation. However it can also be expressed in terms of the integral form $I=\int\limits_{0}^{R}{{{r}^{2}}dm}$

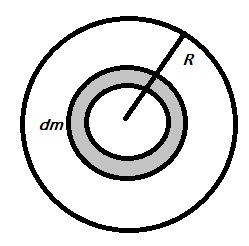
Here, given that the mass $M$ and radius $R$,
Then, moment of inertia is $I_{disc}=\int_{0}^{R} r^{2}(dm)=\int_{0}^{R} r^{2}(\sigma2\pi rdr)$
Where, total mass$M$ is the product of the mass per unit area $\sigma(r)$ times the total area of disc is $2\pi r$
And $\sigma(r)=kr^{2}$ where $r$ is the distance from its centre.
Then, $I_{disc}=\int_{0}^{R}2\sigma\pi r^{3}dr=\int_{0}^{R}2\pi(kr^{2})r^{3}dr=\int_{0}^{R}2\pi kr^{5}dr=2k\int_{0}^{R}\pi r^{5}dr$
Then, we get, $I_{disc}=2k\pi\int_{0}^{R}r^{5}dr=2k\pi\left(\dfrac{r^{6}}{6}\right)_{0}^{R}$
Substituting for $r=R$ and $r=0$
Then,$I_{disc}=2k\pi\left(\dfrac{R^{6}}{6}-0\right)=2k\pi\dfrac{R^{6}}{6}$

We know that the moment of inertia depends mainly on the mass of the object and its distance from the axis of rotation.
But here we are getting the answer in terms of $R$ and$k$, in order to remove $k$, we can find the total mass of the body.
Which is given as, $M=\int_{0}^{R} \sigma (2\pi r)=2k\pi\int_{0}^{R} r^{3}=2k\pi\left[\dfrac{R^{4}}{4}\right]$
Rearranging we get,$k=\dfrac{4M}{2\pi R^{4}}$
Then, substituting the value of $k$ in $I_{disc}$, we get, $I=\dfrac{2\pi\times 4M}{2\pi R^{4}}\times \dfrac{R^{6}}{6}=\dfrac{2MR^{2}}{3}$

So, the correct answer is “Option B”.

Note:
The moment of inertia depends on the density of the material, the axis of rotation and the dimensions of the body, i.e. the shape and the size of the body. Its dimensional formula is given as $[M^{1}L^{2}T^{0}]$ with SI unit is $kgm^{2}$.