Question

A thin dielectric rod of length $l$ lies along the x-axis. one end of the rod is placed at the origin and the other end of the rod is placed at $(l,0)$. A total change $Q$ is distributed uniformly along the length of the rod. what is the potential at a point $(x,0)$ when $x > l$?

Answer 1

It is given that the charge is distributed along the whole length of the rod. This means we need to find the differential potential at the required point due to a small differential length of the rod. Finally, we will integrate this differential potential along the required length to get the answer.

Formula used:
$dV=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{dQ}{r}$

Complete answer:
According to question the rod is placed on the axis as shown in the diagram below:

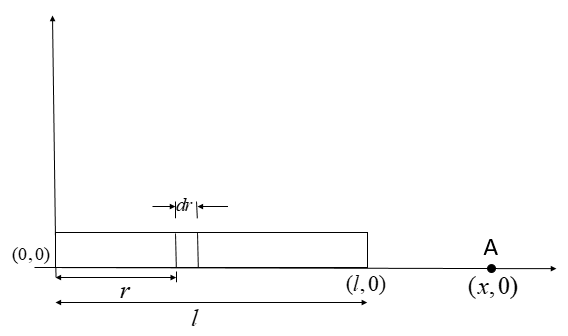
Here, as the charge is distributed along the whole length of the rod, hence we need to find the required potential using integration.
Consider, a small part $dr$ of the rod at a distance $r$ from the origin. Let this part contain a charge $dQ$.
Also, let the charge per unit length be denoted by $\lambda$
We know $\lambda$ is given by:
$\lambda =\dfrac{Q}{l}$ ------(i)
Hence, $dQ$ can be given as:
$dQ=\lambda dr$ ------(ii)
Also, we know that the differential potential due to the part $dr$ is given by:
$dV=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{dQ}{r}$
Using equation (ii)
$dV=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{\lambda dr}{r}$ -----(iii)
Now, to find the potential at point A, we need to integrate this expression from $x$ to $x-l$ as:
$\int{dV}=\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}}\int\limits_{x}^{x-l}{\dfrac{dr}{r}}$
$\Rightarrow V=\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}}\left[ \ln r \right]_{x}^{x-l}$
$\Rightarrow V=\dfrac{\lambda }{4\pi {{\varepsilon }_{0}}}\ln \left( \dfrac{x-l}{x} \right)$
Using equation (i), we get:
$V=\dfrac{Q}{4\pi {{\varepsilon }_{0}}l}\ln \left( \dfrac{x-l}{x} \right)$
Hence the required solution is: $V=\dfrac{Q}{4\pi {{\varepsilon }_{0}}l}\ln \left( \dfrac{x-l}{x} \right)$

Note:
Integrate the differential expression of the voltage from $x-l$ to $x$. Although, it is not wrong if you integrate from $x$ to $x-l$. The only difference is that, in the latter case we will get the final result with a negative sign. This only depicts that as you move away from the rod, the potential decreases.