Question

A thin convex lens L (refractive index= 1.5) is placed on a plane mirror M. When a pin is placed at A, such that OA= 18 cm, its real inverted image is formed at A itself, as shown in figure. When a liquid of refractive index ${\mu}_{1}$ is put between the lens and the mirror. The pin has to be moved to ${A}^{‘}$, such that $O{A}^{‘}$= 27 cm, to get its inverted image at ${A}^{‘}$ itself. The value of ${\mu}_{1}$ will be?
A. $\sqrt {2}$
B. $\dfrac {4}{3}4$
C. $\sqrt {3}$
D. $\dfrac {3}{2}$

Answer 1

To solve this problem, first find the focal length of the convex lens. Then, find the focal length of the surface between the convex lens and the plane mirror M. Now, use the formula for the combination of focal length for convex lens and a plane mirror. Substitute the values in above formula where the focal length f is distance $O{A}^{‘}$ which is 27 m. Solve the equation and find the refractive index of the liquid.
Formula used:
$\dfrac {1}{f}= (\mu – 1) (\dfrac {1}{{R}_{1}}- \dfrac {1}{{R}_{2}})$

Complete answer:

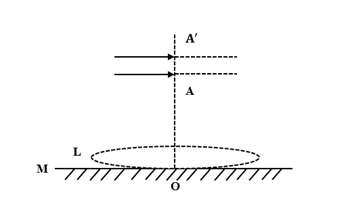
Given: $\mu$= 1.5
Focal length (f)= 27 cm
Lens maker’s formula is given by,
$\dfrac {1}{f}= (\mu – 1) (\dfrac {1}{{R}_{1}}- \dfrac {1}{{R}_{2}})$ …(1)
Focal length of convex lens will be given by,,
$\dfrac {1}{{f}_{1}}= (1.5-1)(\dfrac {1}{18}-\dfrac {1}{-18})$
$\Rightarrow \dfrac {1}{{f}_{1}}= 0.5(\dfrac {1}{18}+\dfrac {1}{18})$
$\Rightarrow \dfrac {1}{{f}_{1}}=0.5 \times \dfrac {2}{18}$
$\Rightarrow \dfrac {1}{{f}_{1}}= \dfrac {1}{2} \times {2}{18}$
$\Rightarrow \dfrac {1}{{f}_{1}}= \dfrac {1}{18}$
Similarly. substituting values in the equation. (1) for ${\mu}_{1}$ we get,
$\dfrac {1}{{f}_{2}}= ({\mu}_{1}-1)(\dfrac {1}{-18}-\dfrac {1}{\infty})$
$\Rightarrow \dfrac {1}{{f}_{2}}= \dfrac {({\mu}_{1}-1)}{-18}$
When liquid of ${\mu}_{1}$ is placed between lens and mirror,
$\dfrac {1}{f}= \dfrac {1}{{f}_{1}}+\dfrac {1}{{f}_{2}}$
Substituting values in above equation we get,
$\dfrac {1}{27}= \dfrac {1}{18}+ \dfrac {({\mu}_{1}-1)}{-18}$
$\Rightarrow \dfrac {1}{27}= \dfrac {1}{18}- ( \dfrac {({\mu}_{1}-1)}{18})$
$\Rightarrow \dfrac {1}{27}= \dfrac {2 –{\mu}_{1}}{18}$
$\Rightarrow 2 – {\mu}_{1}= \dfrac {18}{27}$
$\Rightarrow 2 – {\mu}_{1}= \dfrac {2}{3}$
$\Rightarrow {\mu}_{1}= 2- \dfrac {2}{3}$
$\Rightarrow {\mu}_{1}= \dfrac {4}{3}$
Hence, the value of ${\mu}_{1}$ will be $\dfrac {4}{3}$.

So, the correct answer is “Option b”.

Note:
There is a specific sign convention defined for a given kind of system. Students must be very careful while handling the signs. If it is asked to find the focal length or something related to focal length students should always cross-check with the type of mirror or lens. If the object is placed in front and at the left side, then all the distances to the right of the lens or mirror is positive and the distance on the left are negative.