Question

A thin converging lens is made up of a glass of refractive index 1.5. It acts like a concave lens of focal length 50cm when immersed in a liquid of refractive index$\left( \dfrac{15}{8} \right)$ . The focal length of the converging lens in air is (in m)
A. 0.15
B. 0.20
C. 0.25
D. 0.40

Answer 1

As a first step, you could recall the lens maker’s formula for a lens. Then you could find the lens maker’s formula for air and the liquid separately. After that, you could find the ratio of both and then find the focal length of the lens in air. Also convert the unit of focal length into meters.
Formula used:
Lens maker’s formula,
$\dfrac{1}{f}=\left( {{n}_{21}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$

Complete answer:
We are given a thin converging lens that is made up of glass of refractive index 1.5. This converging lens when immersed in a liquid of refractive index $\dfrac{15}{8}$ behaves like a concave lens (diverging lens) of focal length 50 cm. We are asked to find the focal length of this converging lens in air.
We could use the lens maker’s formula in order to solve this problem.

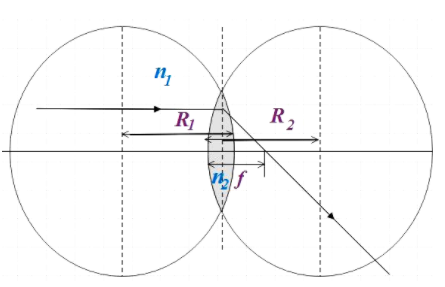
The lens maker’s formula is given by,
$\dfrac{1}{f}=\left( {{n}_{21}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$ …………………………. (1)
Where,
f= focal length of the lens
${{n}_{21}}=\dfrac{{{n}_{2}}}{{{n}_{1}}}$ = relative refractive index of medium 2 with respect to medium 1
${{R}_{1}}$ , ${{R}_{2}}$ are the radius of curvatures of the circles of which the lens for a part.
When the lens is kept in air,
${{n}_{2}}$ = refractive index of lens = 1.5
${{n}_{1}}$ = refractive index of air = 1
So, lens maker’s formula is given by,
$\Rightarrow \dfrac{1}{{{f}_{a}}}=\left( \dfrac{1.5}{1}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$ …………………………… (2)
Where, ‘${{f}_{a}}$’ is the focal length of a lens in air.
When the lens is immersed in liquid, ‘${{n}_{1}}$’ becomes$\dfrac{15}{8}$ .
Lens maker’s formula now becomes,
$\Rightarrow \dfrac{1}{{{f}_{l}}}=\left( \dfrac{1.5}{\dfrac{15}{8}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$ …………………………… (3)
Where, ‘${{f}_{l}}$’ is the focal length of the lens in the liquid.
Dividing (4) by (3) gives,
$\Rightarrow \dfrac{\dfrac{1}{{{f}_{l}}}}{\dfrac{1}{{{f}_{a}}}}=\dfrac{\left( \dfrac{1.5}{\dfrac{15}{8}}-1 \right)}{\left( \dfrac{1.5}{1}-1 \right)}$
$\Rightarrow \dfrac{{{f}_{a}}}{{{f}_{l}}}=\dfrac{\left( \dfrac{1.5-1.875}{1.875} \right)}{0.5}=-\dfrac{0.2}{0.5}=-0.4$
$\Rightarrow {{f}_{a}}=-0.4\times {{f}_{l}}$
From the question,
${{f}_{l}}=-50cm$
$\Rightarrow {{f}_{a}}=-0.4\times -50cm=20cm$
Therefore, the focal length of the converging lens in air is (in m) 0.2m.

Hence, the answer to the given question is option B.

Note:
We are given that the lens acts as a concave lens, that is, a diverging lens when immersed in the liquid. By sign convention we know that the focal length of the concave lens is taken negative and that is the reason why we have substituted -50 cm in place of the focal length of the lens in the liquid. Also, remember to convert the value in units as asked in the question.