Question

A thin concavo-convex lens has two surfaces of radii of curvature R and 2R. The material of the lens has a refractive index $\mu$. When kept in air, the focal length of the lens
A. Will depend on the direction from which light is incident on it
B. Will be the same, irrespective of the direction from which light is incident on it
C. Will be equal to $\dfrac{R}{{\mu - 1}}$
D. Will be equal to $\dfrac{{2R}}{{\mu - 1}}$

Answer 1

As here we have to find the focal length of a thin concavo – convex lens whose radii of curvatures are given so it can be solved by using lens maker’s formula for thin lenses.
Formula used: Lens maker formula for thin – lenses is given by
$\dfrac{1}{f} = \left( {\mu - 1} \right)\left[ {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right]$
Where f is the focal length of a thin lens, $\mu$is its refractive index of lens, ${R_1}$and ${R_2}$ are the radii of curvature.

Complete step by step answer:
We know that a thin concavo convex lens with light from left to right is given by the figure below

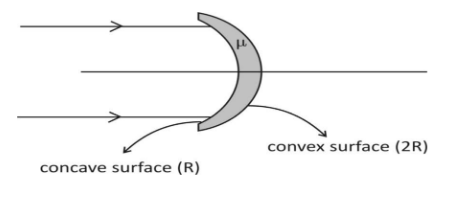
For light from left to right, the radii of curvature of first surface $= {R_1} = - R$
The radii of curvature of second surface $= {R_2} = - 2R$
Refractive index of material of lens $= \mu$
So, in this case, the focal length of the lens by lens maker formula is given by
\dfrac{1}{{{f_1}}} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right) \\\ \dfrac{1}{{{F_1}}} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{ - R}}\dfrac{{ - 1}}{{ - 2R}}} \right) \\\ = \left( {\mu - 1} \right)\left( {\dfrac{1}{{2R}} - \dfrac{1}{R}} \right) = \left( {\mu - 1} \right)\left( {\dfrac{{1 - 2}}{{2R}}} \right) \\\ \dfrac{1}{{{f_1}}} = \left( {\mu - 1} \right)\left( {\dfrac{{ - 1}}{{2R}}} \right) \\\
$\dfrac{1}{{{f_1}}} = - \left( {\mu - 1} \right)\left( {\dfrac{1}{{2R}}} \right)$ … (i)
When the light is incident from right to left in this concavo-convex lens, then as the given figure below we have

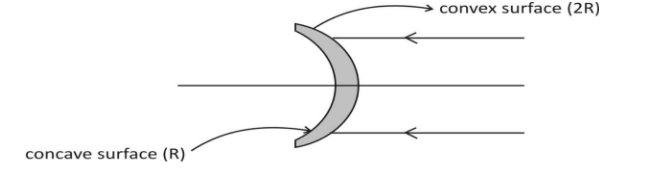
For light from right to left,
The radii of curvature of first surface $= {R_1} = R$
The radii of curvature of second surface $= {R_2} = R$
So, the focal length, ${f_2}$, in this case by lens maker’s formula will be given by
$\dfrac{1}{{{f_2}}} = \left( {\mu - 1} \right)\left( {\dfrac{1}{{2R}} - \dfrac{1}{R}} \right)$
$\dfrac{1}{{{f_2}}} = - \dfrac{{\left( {\mu - 1} \right)}}{{2R}}$… (ii)
From (i) and (ii), it is clear that
$\dfrac{1}{{{f_1}}} = \dfrac{1}{{{f_2}}} = - \dfrac{{\left( {\mu - 1} \right)}}{{2R}}$
$\Rightarrow$Focal length, ${f_1} = {f_2} = \dfrac{{ - 2R}}{{\left( {\mu - 1} \right)}}$
Hence, option (D) is the correct option.

Note: : In case of incident light from left to right, then
${R_1} = - R$and ${R_2} = - 2R$
It is negative because here the distances ${R_1}$and ${R_2}$are measured against the direction of incident light.
When light is incident from right to left, then
${R_1} = + 2R,{\text{ }}{{\text{R}}_2} = + R$
Both are positive as both being measured in direction of incident light.