Question

A thin circular plate of mass M and radius R has its density varying as $\rho (r) = {\rho _0}r$ with ${\rho _0}$ as constant and r is the distance from its centre. The moment of inertia of the circular plate about an axis perpendicular to the plate and passing through its edge is $I = aM{R^2}.$ the value of the coefficient a is:
A. $\dfrac{3}{2}$
B. $\dfrac{1}{2}$.
C. $\dfrac{3}{5}$.
D. $\dfrac{8}{5}$.

Answer 1

In this question, we will use the concept of moment of inertia of a body. We should know that the moment of inertia of a rigid body around a fixed axis is defined as the sum of the products of the masses of the particles that make up the body and the squares of their respective distances from the rotation axis, i.e. $I = {m_1}{r_1}^2 + {m_2}{r_2}^2 + {m_3}{r_3}^2 + ........$
$I = \sum\limits_{i = 1}^n {{m_i}{r_i}^2}$.

Formula used: $\rho = \dfrac{{mass}}{{area}}$, area of circle = $2\pi rdr$, $I = {I_{CM}} + M{R^2}$.

Complete step-by-step answer:

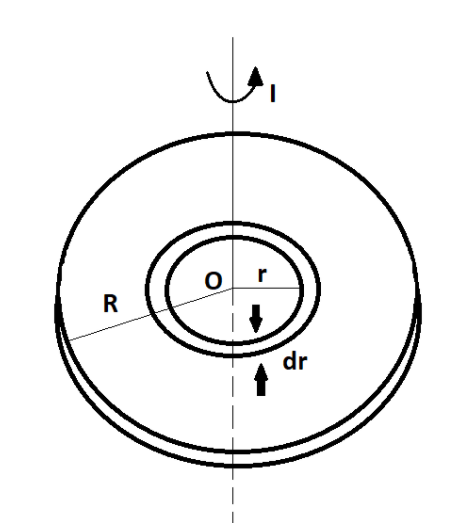
Given that, M is the mass and R is the radius of the plate, varying density as $\rho (r) = {\rho _0}r$ where ${\rho _0}$ as constant and r is the distance from its centre.
Taking a circular ring of radius r and thickness $dr$ as a mass element, then
Area of circular ring = $2\pi rdr$.
We know that, density = $\rho = \dfrac{{mass}}{{area}}$.
Then, mass = $\rho \times area$. …………………….……..(i)
So for total mass, we will integrate equation (i) with limit 0 to R, we get
$\Rightarrow M = \int\limits_0^R {{\rho _0}r \times } 2\pi rdr \\\ \Rightarrow M = \left[ {\dfrac{{{r^3}}}{3}} \right]_0^R \times 2\pi {\rho _0} \\\ \Rightarrow M = \dfrac{{2\pi {\rho _0}{R^3}}}{3} ………………….(ii)$
Let ${I_{CM}}$be the moment of inertia of the body about the axis parallel to the perpendicular axis,
We know that, ${I_{CM}} = {\text{total mass}} \times {{\text{r}}^2}$, then
${I_{CM}} = \int\limits_0^R {{\rho _0}r \times } 2\pi rdr \times {r^2}$, we get
${I_{CM}} = \dfrac{{2\pi {\rho _0}{R^5}}}{5}.$
Now, using the parallel axis theorem, we know that

\Rightarrow I = {I_{CM}} + M{R^2} \\\ \Rightarrow I = \dfrac{{2\pi {\rho _0}{R^5}}}{5} + \dfrac{{2\pi {\rho _0}{R^3}}}{3} \times {R^2} \\\ \Rightarrow I = \dfrac{{2\pi {\rho _0}{R^5}}}{5} + \dfrac{{2\pi {\rho _0}{R^5}}}{3} = 2\pi {\rho _0}{R^5}\left[ {\dfrac{1}{5} + \dfrac{1}{3}} \right] \\\ \Rightarrow I = 2\pi {\rho _0}{R^5} \times \dfrac{8}{{15}} = \dfrac{{16\pi {\rho _0}{R^5}}}{{15}} \\\ \Rightarrow I = \dfrac{8}{5}\left[ {\dfrac{{2\pi {\rho _0}{R^3}}}{3}} \right]\times{R^{2}} \\\ \Rightarrow I = \dfrac{8}{5}M{R^2} ………………\text{by equation}(ii) $$ Now comparing this with $I = aM{R^2}$, we get $ \Rightarrow a = \dfrac{8}{5}$. **Hence, the correct answer is option(D).** **Note:** In this type of questions, we should have some basic knowledge of the moment of inertia of a body. Then we will find out the elementary mass by using the given density and area of the ring. After that we will put this value to find the total mass. Then we will use the theorem of parallel axis to find out the moment of inertia. Solving it step by step, we will get the required answer.