Question

A thin circular loop of radius $R$ rotates about its vertical diameter with an angular frequency $\omega$. Show that a small bead on the wire loop remains at its lowest point for $\omega \leqslant \sqrt {g/R}$. What is the angle made by the radius vector joining the center to the bead with the vertically downward direction for $\omega = \sqrt {2g/R}$ ? Neglect friction.

Answer 1

First, you have to understand the system represented in the question. A bead is rotating with a radius and angular frequency. If the angular frequency $\omega$ is less than the square root of gravity divided by radius, which means the bead is at rest position. If the angular frequency is equal to the square root of two-time gravity divided by radius means how many angles the bead will make to the origin, it is the question. Here the picture represents the system and question.

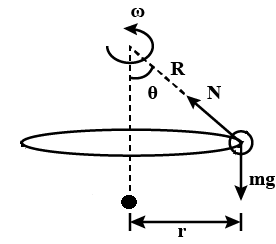
Complete answer:
The normal force $N$ for the horizontal component is equal to the angular force acting on the bead,
$N\sin \theta = mr{\omega ^2}$-------1
We can write $r$ as,
$r = R\sin \theta$
Substitute this into equation 1, we get,
$N\sin \theta = mR\sin \theta {\omega ^2}$--------2
The normal force $N$ for the vertical component is equal to the downward force acting on the bead,
$N\cos \theta = mg$-------3
Divide the equation 3 by eq 2, we get,
$\cos \theta = \dfrac{{mg}}{{mR{\omega ^2}}}$
$\cos \theta = \dfrac{g}{{R{\omega ^2}}}$
We need $\omega$ only, so we get,
$\omega = \sqrt {\dfrac{g}{{R\cos \theta }}}$--------4
At the rest position $\theta = 0$ means,
$\omega = \sqrt {\dfrac{g}{R}}$
Substitute $\omega = \sqrt {\dfrac{{2g}}{R}}$, we get,
$\cos \theta = \dfrac{1}{2}$
$\theta = 60{}^0$

Note:
The angle $\theta$ will always be in the range of ${0^0} \leqslant \theta < {90^0}$. The angle cannot be greater than ${90^0}$. Because the maximum rotation of the bead will make the maximum angle less than ${90^0}$. The gravity is greater than the angular frequency means, the bead is at rest position because the angular velocity didn't have much efficiency to move the bead due to the interaction of gravity.