Solveeit Logo
Login

Question

Question: A thin bar magnet of length 2L is bent at the mid-point so that the angle between them is \({60^ \ci...

A thin bar magnet of length 2L is bent at the mid-point so that the angle between them is 60∘{60^ \circ }. The new length of the magnet:
\eqalign{ & {\text{A}}.\;\sqrt 2 L \cr & {\text{B}}.\;\sqrt 3 L \cr & {\text{C}}.\;\;2L \cr & {\text{D}}.\;\;L \cr}

Explanation

Solution

The length of any magnet is the distance between it’s north and south pole. On bending a bar magnet, only the magnetic length changes and there’s no effect on the pole strength of the magnet. Hence the magnetic moment, which is the ratio of pole strength and length of magnet, will also change accordingly.

Formula used:
Basic properties of the triangle and Angle sum property i.e. in Δ\Delta ABC,
∠A+∠B+∠C  =  180∘\angle A + \angle B + \angle C\; = \;{180^ \circ }

Complete step-by-step answer:
Given the length of the magnet is 2L. Bending it in the middle will make two sides of a triangle as shown in the figure.

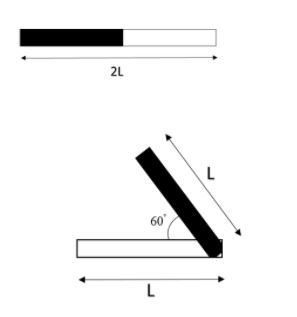
Now, as the two sides of the triangle are equal, hence its opposite angles are also equal (Property of isosceles triangle).

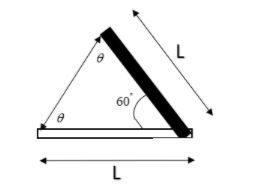
Now, by angle sum property, ∠A+∠B+∠C  =  180∘\angle A + \angle B + \angle C\; = \;{180^ \circ }
Putting the values of angles, we get
\eqalign{ & \Rightarrow \theta + \theta + {60^ \circ } = {180^ \circ } \cr & \Rightarrow 2\theta = {120^ \circ } \cr}
Hence, θ=60∘\theta = {60^ \circ }
So, it’s an equilateral triangle. Means it has all three sides equal. Hence the third side of the triangle is also equal to L.

So, the correct answer is “Option D”.

Additional Information: Students should note that it’s not always necessary that the angle is 60∘{60^ \circ } or the triangle is an isosceles/equilateral. In that scenario, it is advised to go with a vector method which says treat both lengths as two vectors and assume the angle between them as given so resultant will give the length of the magnet. Now suppose, the angle is 0∘{0^ \circ }, it means that the magnet is attached side by side. In that case, the length will be half of the original length and not 0 units, as in that case, the poles will combine.

Note: One can also apply the cosine formula here. Since we know the length of two sides and the angle between them. Always remember that the geometric length of a magnet is always a little greater than the magnetic length because it always assumed that the poles of the magnet lie a little bit inside the material.