Question

A thief moving on a bike with uniform velocity passes a stationary policeman who is hiding behind a billboard with a motorcycle. After a 2.0 sec delay (reaction time) the policeman accelerates to his maximum speed 150 km/hr. in 12 seconds. The policeman moves with uniform speed of 150 km/hr from this instant onwards and catches up with the thief 1.5 km beyond the billboard. Find the speed of the thief in km/hr.

Answer 1

In this question, we are asked to calculate the speed of the thief in km/hr. It is given that the thief was caught after 1.5 km. We know, speed is given as distance travelled over time taken. Therefore, we will first calculate the time required by the policeman to catch the thief. To solve this question, we shall be using a graphical method.

Complete step by step answer:
It is given that the policeman takes 2 seconds of reaction time and reaches the maximum speed after 12 seconds. Therefore, the total time required for a policeman to reach his maximum speed, including the reaction timing is 14 seconds as shown in the figure below.

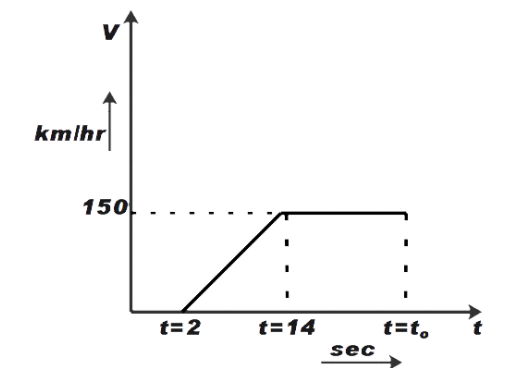
Now, the distance travelled by the policeman while obtaining his maximum speed can be given the area under the curve t=2 to t=14 seconds and speed of 150 km/hr.
Therefore, from above graph we can say that
$d=\dfrac{1}{2}\times 150\times \dfrac{12}{3600}$ ……………… (converting seconds to hours)
Therefore,
$d=0.25km$
Now, it is given that the thief was caught by the policeman after 1.5 km. This is the total distance travelled by a policeman. Therefore, distance travelled by the policeman with constant speed can be said to be
$d=1.5-0.25$
Therefore,
$d=1.25km$
Now, we know that a policeman travelled 1.25 km with a constant speed of 150 km/hr. Therefore, the time required to travel this distance is given by,
${{t}_{o}}=\dfrac{1.25}{150}$
Therefore,
${{t}_{o}}=30\sec$
Now from the graph, we can say that total time required for the policeman to catch the thief is
$t=14+30$
Therefore,
$t=44\sec$
Now, it is given that the total distance travelled by the thief is 1.5 km and the total time before he was caught is 44 seconds.
Therefore, the speed of the thief will be given by,
$s=\dfrac{1.5}{{}^{44}/{}_{3600}}$ …………….. (converting time from seconds to hours)
On solving
We get,
$s=122.7km/hr$

So, the correct answer is “s=122.7km/hr”.

Note: This question can be solved by using kinematic equations as well. We will first calculate the total time required by the policeman to catch the thief. We will then calculate the distance travelled by the policeman before reaching maximum speed to the time he caught the thief. Now, we know that the time taken by the policeman to catch the thief will be equal to the time taken by the thief to cover a given distance of 1.5 km. Therefore, in such a way the speed of the thief can be calculated.