Question

A thief is running away in a car with velocity of $20m/s$. A police jeep is following him, which is sighted by a thief in his rear-view mirror which is a convex mirror of focal length $10m$. He observes that the image of the jeep is moving towards him with a velocity of $1cm/s$. If the magnification of the mirror of the jeep at that time is $\dfrac{1}{10}$. The police jeep is on the axis of the mirror. Find the actual speed of the jeep.

Answer 1

Hint: The velocities of the mirror, the object and the magnification of the mirror are known. From the velocity formula, use the velocity of the image with respect to the mirror and find the velocity of the object with respect to the mirror. Thus, finding the velocity of the jeep with respect to ground.

Complete solution:
The focal length of the mirror, f, is given as
$f=+10m$. From this, you can infer that the mirror is convex in nature. That is the image formed will always be erect, diminished.
The thief is sitting in the car, where the mirror is installed. That is the velocity of mirror and the car with respect to ground become:

${{V}_{cg}}={{V}_{mg}}=20m/s$.

The police are the jeep. The velocity of the jeep with respect to the ground, which is the object velocity ${{V}_{om}}$, has to be calculated. But, the velocity of jeep with respect to the mirror, which is the image velocity ${{V}_{im}}$, is given as:
${{V}_{im}}=-1cm/s=-\dfrac{1}{100}m/s$. It is negative, as the positive direction is assumed to be the direction of motion of the car. And, the velocity of the image in the mirror is in the opposite direction.

The magnification, m of the mirror is given as:

$m=\dfrac{1}{10}$

We know, that the mirror formula is given by:

& \dfrac{1}{v}+\dfrac{1}{u}=\dfrac{1}{f} \\\ & \text{Where, v is the displacement of the image form the mirror} \\\ & \text{u is the displacement of the object form the mirror,} \\\ & \text{and f is the focal length of the mirror}\text{.} \\\ \end{aligned}$$ Now, differentiating this equation with respect to time: $\dfrac{d}{dt}\dfrac{1}{v}+\dfrac{d}{dt}\dfrac{1}{u}=\dfrac{d}{dt}\dfrac{1}{f}$ Where, f is a constant $-\dfrac{1}{{{v}^{2}}}\dfrac{dv}{dt}-\dfrac{1}{{{u}^{2}}}\dfrac{du}{dt}=0\text{ }...\text{(1)}$ Now, the velocity of the image wrt mirror will be: ${{V}_{im}}\text{=}\dfrac{dv}{dt}\text{,}$ Similarly, the velocity of the object wrt mirror will be: ${{\text{V}}_{om}}=\dfrac{du}{dt}$ Therefore, equation (1) reduces to: ${{V}_{im}}=-\dfrac{{{v}^{2}}}{{{u}^{2}}}{{V}_{om}}$ And the magnification m is given by: $m=-\dfrac{v}{u}$ Therefore: ${{V}_{im}}=-{{m}^{2}}{{V}_{om}}$ Let the velocity of the jeep with respect to the mirror, ${{V}_{om}}$. Consider the velocity formula: $$\begin{aligned} & {{V}_{im}}=-{{m}^{2}}{{V}_{om}} \\\ & \Rightarrow -\dfrac{1}{100}=-\dfrac{1}{100}{{V}_{om}} \\\ & \Rightarrow {{V}_{om}}=+1m/s \\\ \end{aligned}$$ That is, the velocity of the object, which is the jeep, is $$+1m/s$$ in the same direction as that of the car of the thief. We know that ${{V}_{cg}}=20m/s$, the velocity of a car with respect to ground. 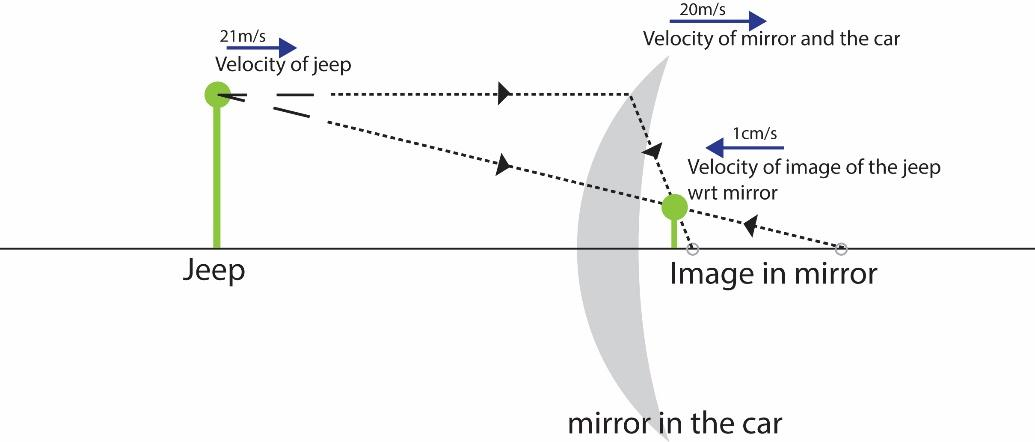 Therefore, by vector addition: $\begin{aligned} & {{V}_{og}}={{V}_{om}}+{{V}_{mg}} \\\ & {{V}_{og}}=1+20=21m/s \\\ \end{aligned}$ Hence the actual speed of the jeep is 21m/s. Note: Relation between focal length and velocity becomes really important when considered in optics. As the focal length of the mirror determines if the mirror is concave or convex, and the nature of the image formed subsequently. A convex mirror has a positive focal length, whereas a concave mirror has a negative focal length.