Question

A thick uniform wire is bent into the shape of the letter U as shown. Which point indicates the location of the centre of mass of this wire? (approximately)

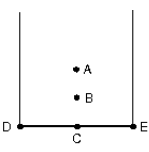
A. $A$
B. $B$
C. $C$
D. $D$

Answer 1

The centre of mass of a mass distribution in space is the unique place in space where the weighted relative position of the distributed mass accumulates to zero, according to physics. A force can be applied to this point to induce a linear acceleration without causing an angular acceleration.

Complete step by step answer:
Point $B$ is right because it is on the line that runs parallel to and in the middle of the two parallel arms, as well as because it shifts from the parallel arms' COM towards the base, as it should because the base has a finite mass. The system has three rods, for the first rod (along x-axis) the centre of mass of this rod is at $\left( {\dfrac{C}{2},0} \right)$.

For the second rod (along y-axis) the centre of mass of this rod is at $\left( {0,\dfrac{C}{2}} \right)$ while for the third rod the centre of mass is at $\left( {\dfrac{C}{2},C} \right)$. Let us assume the mass of each rod to be $m$ . thus the centre of mass of the system is at:
${X_{com}} = \dfrac{{{m_1}{x_1} + {m_2}{x_{2 + }}{m_3}{x_3}}}{{{m_1} + {m_2} + {m_3}}}$
So, we have ${m_1} = {m_2} = {m_3} = m$
So ${X_{com}} = \dfrac{{m\dfrac{C}{2} + 0 + m\dfrac{C}{2}}}{{3m}} = \dfrac{C}{3}$
Similarly, ${Y_{com}} = \dfrac{{{m_1}{y_1} + {m_2}{y_2} + {m_3}{y_3}}}{{{m_1} + {m_2} + {m_3}}}$
So, we have ${m_1} = {m_2} = {m_3} = m$
${Y_{com}} = \dfrac{{0 + m\dfrac{C}{2} + mL}}{{3m}} = \dfrac{C}{2}$
So, coordinates of COM = $\left( {\dfrac{C}{3},\dfrac{C}{2}} \right)$
At last, $B$ is the point mentioned.

So, the correct option is B.

Note: Because it must be symmetrically between the two parallel sides, Point D cannot be the Centre of Mass. (the system is symmetrical about a line parallel to and midway between the parallel arms of the U-wire).Because the wire is uniform, Point C cannot be the Centre of Mass because it implies that the masses of the parallel arms are zero. Point A can't be the Centre of Mass because it implies that the base's mass is zero, which isn't the case