Question
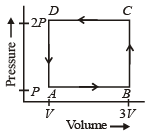
Question: A thermodynamic system is taken through the cycle ABCD as shown in the figure. Heat rejected by the ...
A thermodynamic system is taken through the cycle ABCD as shown in the figure. Heat rejected by the gas during the cycle is:
(a)PV(b)2PV(c)4PV(d)21PV
Solution
The given thermodynamic system has been performed in a cyclic manner. And we know that, in a cyclic process the initial internal energy of the system is equal to the final internal energy of the system. This means that the net change in the internal energy of the system over a cyclic process is zero. So, the total work performed by the system will be equal to the heat released or absorbed by the system depending on the work.
Complete step by step answer:
The given thermodynamic system is first taken from (A→B) which is an isobaric process. The work done in this process is:
⇒WAB=P(3V−V)⇒WAB=2PV
Then, it is taken from (B→C), which is an isochoric process. Thus, work done in taking the system from (B→C) is zero. That is:
⇒WBC=0
Now, in the third step the system again undergoes an isobaric process from (C→D). Thus,
⇒WCD=2P(V−3V)⇒WCD=−4PV
The last step is again isochoric. Thus,
⇒WDA=0
Therefore, in the complete cycle (A→B→C→D→A) , the net work done can be given by:
⇒Wcycle=WAB+WBC+WCD+WDA⇒Wcycle=2PV+0+(−4PV)+0⇒Wcycle=−2PV
Now, from first law of thermodynamics:
⇒△Q=△U+△W
Here, we have:
⇒△U=0 and,
⇒△W=Wcycle=−2PV
Thus, putting these values in above equation we get:
⇒△Q=0+(−2PV)⇒△Q=−2PV
This is the heat absorbed by the system.
Therefore, heat rejected by the system is equal to 2PV
So, the correct answer is “Option b”.
Note: In a cyclic process, we can very easily determine the sign of work using a simple trick. The total work done in the cyclic process is positive if the nature of the cycle is clockwise and if the process is performed in counter-clockwise direction, then the net work done is negative. Once the sign of the net work is known, we can easily calculate the magnitude of net work by finding the area bounded by the cycle.
