Question

A: The smallest possible radius of circle which pass through $\left( 1,0 \right)$and $\left( 0,1 \right)$ is $\dfrac{1}{\sqrt{2}}$.
R: Circle passes through origin.
a)Both A and R are individually true and R is the correct explanation of A
b)Both A and R are individually true but R not the correct explanation of A
c)A is true but r is false
d)A is false but R is true

Answer 1

Hint: Find the slope using the slope point formula which is $m\ =\ \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ where, m is the slope and $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the points. Check if the circle passes through origin or not.

Complete step-by-step answer:

Now, let's consider the circle which passes through points $\text{A}\left( 1,0 \right)$ and $\text{B}\left( 0,1 \right)$ and also the origin.

Let’s consider the circle to have the smallest possible length of AB. It should be the diameter of the circle.

Assuming point $\text{P}\left( x,y \right)$ be any point on the circumference of the circle, we can say that $\angle APB$ is $90{}^\circ$because there is property of the circle that angle contained in semicircle is $90{}^\circ$.

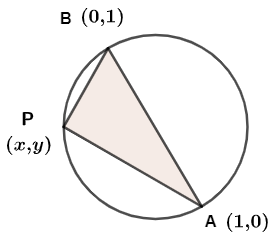
Let’s find the slope of AP by the formula ${{m}_{1}}\ =\ \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ where ${{m}_{1}}$ is slope of AP and $\left( {{x}_{1}},{{y}_{1}} \right)$ is $\left( 1,0 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( x,y \right)$.

So, ${{m}_{1}}\ =\ \dfrac{y-0}{x-1}\ =\ \dfrac{y}{x-1}$

Now, let’s find the slope of BP by the formula ${{m}_{2}}\ =\ \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ where ${{m}_{2}}$is slope of BP and $\left( {{x}_{1}},{{y}_{1}} \right)$ is $\left( 0,1 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( x,y \right)$.

So, ${{m}_{2}}\ =\ \dfrac{y-1}{x-0}\ =\ \dfrac{y-1}{x}$

Here, we know the $\angle APB\ =\ {{90}^{\circ }}$ so AP and BP are perpendicular to each other.

So, ${{m}_{1}}\times {{m}_{2}}\ =\ -1$

$\Rightarrow \ \dfrac{y}{\left( x-1 \right)}\times \dfrac{y-1}{x}\ =\ -1$

$\Rightarrow \ \dfrac{{{y}^{2}}-y}{{{x}^{2}}-x}\ =\ -1$

By cross-multiplication,

$\ {{y}^{2}}-y\ =\ -{{x}^{2}}+x$

Now, taking all the terms to one side we get,

$\ {{x}^{2}}+{{y}^{2}}-x-y\ =\ 0$

Now, adding $\dfrac{1}{2}$to both the sides we get,

$\ {{x}^{2}}-x+\dfrac{1}{4}+{{y}^{2}}-y+\dfrac{1}{4}\ =\ \dfrac{1}{2}$

$\ {{\left( x-\dfrac{1}{2} \right)}^{2}}+{{\left( y-\dfrac{1}{2} \right)}^{2}}\ =\ {{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}$ ………………………………………….(i)

In the equation (i) of circle, the radius of the circle is $\left( \dfrac{1}{\sqrt{2}} \right)$

To prove that the equation (i) of the circle passes through origin we have to substitute $x\ =\ 0$, $y\ =\ 0$ to prove the left hand side and right hand side are equal.

$\ {{\left( x-\dfrac{1}{2} \right)}^{2}}+{{\left( y-\dfrac{1}{2} \right)}^{2}}\ =\ {{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}$

$\ {{\left( \dfrac{1}{2} \right)}^{2}}+{{\left( -\dfrac{1}{2} \right)}^{2}}\ =\ {{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}$

$\ \dfrac{1}{4}+\dfrac{1}{4}\ =\ \dfrac{1}{2}$

$\ \dfrac{1}{2}=\ \dfrac{1}{2}$

Hence the left-hand side and right-hand side are equal.

Now we know that both the statements ‘A’ and ‘R’ are true so the option ‘c’ and ‘d’ are false. ‘R’ statement is the correct explanation of ‘A’.

So, the answer is ‘a’.

Note: The student might have confusion about taking AB as diameter.