Question

(a) The potential difference applied across a given resistor is altered so that the heat produced per second increases by a factor$9$. By what factor does the applied potential difference change?
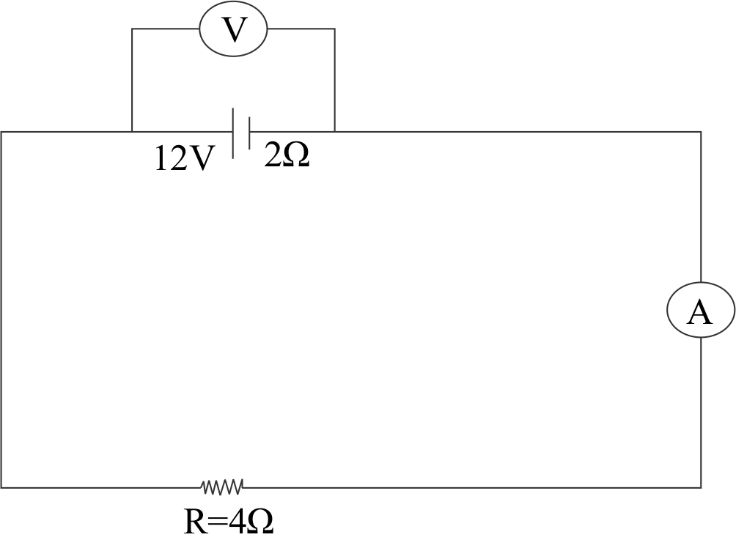
(b) In the figure shown, an ammeter A and a resistor are $4\Omega$ connected to the terminals of the source. The emf of the source is $12V$ having an internal resistance $2\Omega$. Calculate the voltmeter and ammeter reading.

Answer 1

Electric potential could be a location-dependent amount that expresses the number of potential energy per unit of charge at such location. Once a Coulomb of charge (or any given quantity of charge) possesses a comparatively great quantity of potential energy at a given location, then that location is alleged to be a location of high electric potential. And equally, if a Coulomb of charge (or any given quantity of charge) possesses a comparatively tiny amount of potential energy at a given location, then that location is alleged to be a location of low electric potential.

Formula used:
Heat produced,
$\Rightarrow H = \dfrac{{{V^2}t}}{R}$
Where, $H$is the heat produced, $V$is the voltage, $t$is the time, and $R$is the resistance.
Voltmeter,
$\Rightarrow V = R - IR$
Where, $R$ is the resistance, and $I$ is the ammeter.

Complete step by Step Solution In this question, the heat is altered and that causes the heat produced by is $9$ times its initial.
So they are asking the factor for which the applied potential difference changes.
$\left( a \right)$. Suppose the original potential difference applied to be $V$ and the original heat produced will be $H$.
Then,
$\Rightarrow H = \dfrac{{{V^2}t}}{R}$
Now the new potential difference will be $V'$ and the heat produced after the change is $H'$
Then, we can write the equation as
$\Rightarrow H' = \dfrac{{{{V'}^2}t}}{R}$
According to the question statement,
$\Rightarrow H' = 9H$
Now we will put the values of both the heat,
We get
$\Rightarrow \dfrac{{{{V'}^2}t}}{R} = 9 \times \dfrac{{{V^2}t}}{R}$
On further solving this equation, we get
$\Rightarrow {V'^2} = 9{V^2}$
Which implies,
$\Rightarrow V' = 3V$
Therefore we can say that the potential difference is increased by a factor $3$.

$\left( b \right)$. Let us consider the voltmeter and the ammeter to be in an ideal state.
Here the total resistance $R$ will be equal to
$\Rightarrow R = 4 + 2$
$\Rightarrow 6\Omega$
Then the ammeter reading will be,
$\Rightarrow I = \dfrac{V}{R}$
$\Rightarrow I = \dfrac{{12}}{6}$
$\Rightarrow 2A$
Hence the ammeter reading will be$2A$.
Now we will calculate the voltmeter required,
$\Rightarrow V = R - IR$
Substituting the values, we get
$\Rightarrow 12 - 2 \times 2$
$\Rightarrow 12 - 4$
$\Rightarrow 8V$

Therefore the voltmeter reading will be $8V$.

Note: Voltmeters and ammeters measure the voltage and current, severally, of a circuit. Some meters in automobile dashboards, digital cameras, cell phones, and tuner-amplifiers are voltmeters or ammeters.