Question

(a) ${\text{200 c}}{{\text{m}}^{\text{3}}}$ of an aqueous solution of a protein contains $1.26{\text{ g}}$ of protein. The osmotic pressure of such a solution at ${\text{300 K}}$ is sound to be ${\text{2}}{\text{.57 }} \times {\text{ 10}}{{\text{ }}^{{\text{ - 3}}}}{\text{ bar}}$ . Calculate molar mass of protein.
(b) Plot a graph of vapour pressure against mole fractions of the two volatile liquids forming an ideal solution

Answer 1

(a) To determine calculate the molar mass from the osmotic pressure, use the following relationship
$M = \dfrac{{w \times R \times T}}{{\Pi \times V}}$
(b) An ideal solution obeys Raoult’s law under all conditions of temperature and pressure.
According to Raoult's Law, the vapour pressure of a solution of non-volatile solute is equal to the product of the pure solvent and the mole fraction of the solvent.

Complete step-by-step solution:
The mass of the protein ${\text{w = }}1.26{\text{ g}}$
The volume of the solution ${\text{V = 200 c}}{{\text{m}}^{\text{3}}} = 0.2{\text{ L}}$
The temperature of the solution ${\text{T = 300 K}}$
The osmotic pressure of the solution $\Pi = {\text{2}}{\text{.57 }} \times {\text{ 10}}{{\text{ }}^{\text{3}}}{\text{ bar}}$
Write the formula for the osmotic pressure of the solution
$\Pi = CRT = \dfrac{{nRT}}{V}$
$\Pi = \dfrac{{wRT}}{{MV}}{\text{ }}\left( {\because n = \dfrac{w}{M}} \right)$
Rearrange the above formula
$M = \dfrac{{w \times R \times T}}{{\Pi \times V}}$
Substitute values in the above formula
$M = \dfrac{{1.26{\text{ g}} \times 0.08206 \times {\text{300 K}}}}{{{\text{2}}{\text{.57 }} \times {\text{ 10}}{{\text{ }}^{{\text{ - 3}}}}{\text{ bar}} \times 0.2{\text{ L}}}}$
$M = 61,039{\text{ g/mol}}$
Hence, the molar mass of the protein is $61,039{\text{ g/mol}}$ .

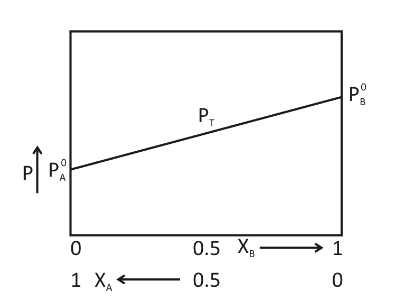
(b)Consider a binary mixture of two liquids A and B
$P_A^o$ and $P_B^o$ are the vapour pressures of pure liquids A and B respectively.
${X_A}$ and ${X_B}$ are the mole fractions of liquids A and B respectively in the solution.
Plot a graph of vapour pressure against mole fractions of the two volatile liquids forming an ideal solution:

Note:(a)Calculating molar mass from osmotic pressure is more accurate than calculating the molar mass from either the elevation in the boiling point or the depression in the freezing point.
(b) For an ideal binary solution containing two components A and B. the expression for the total pressure is as follows.

$${P_T} = {P_A} + {P_B} \\\ {P_T} = {X_A}P_A^o + {X_B}P_B^o \\\ {P_A} = {X_A}P_A^o \\\ {P_B} = {X_B}P_B^o \\\$$