Question

A tetrahedron has vertices at O(0, 0, 0), A(1, -2, 1), B(-2, 1, 1) and C(1, -1, 2). Then the angle between the faces OAB and ABC will be
(a) ${{\cos }^{-1}}\left( \dfrac{1}{2} \right)$
(b) ${{\cos }^{-1}}\left( \dfrac{-1}{6} \right)$
(c) ${{\cos }^{-1}}\left( \dfrac{-1}{3} \right)$
(d) ${{\cos }^{-1}}\left( \dfrac{1}{4} \right)$

Answer 1

Hint: By using the given point find the normals of the required planes. The angle between normals can be found similarly to how we find angles between lines. As the normals are the lines perpendicular to planes. The angle between them will automatically become the angle between the plane which has normals as these lines. So, we got the required angle. If angle between the lines $l:a\hat{i}+b\hat{j}+c\hat{k},m:d\hat{i}+e\hat{j}+f\hat{k}$ (these are the directions) is X, then it is given as
$\cos X=\dfrac{\left( a\hat{i}+b\hat{j}+c\hat{k} \right)\left( d\hat{i}+e\hat{j}+f\hat{k} \right)}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}\sqrt{{{d}^{2}}+{{e}^{2}}+{{f}^{2}}}}$

Complete step-by-step answer:

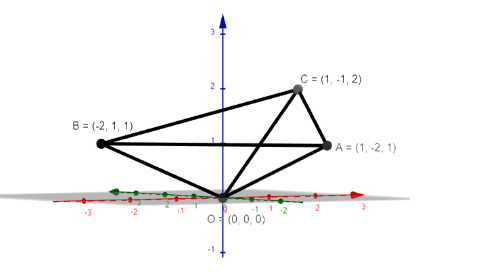
Tetrahedron: In geometry a tetrahedron, also known as a triangular pyramid is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is a special figure as it is the simplest of all possible convex polyhedral and the only one that has fewer than 5 faces. We say its base shape and side shape are triangular (mathematically)

Now, we want an angle between planes OAB, ABC that is nothing but angle between their normal.
Normal of OAB: So, a cross product of any two vectors on this plane will give us normal’s direction.
By above and knowledge, we know that OA, OB lie in this plane. So, the normal is given by direction of

{} & O & A & B \\\ OA\times OB= & \left( 0,0,0 \right) & \left( 1,-2,1 \right) & \left( -2,1,1 \right) \\\ \end{matrix}$$ given in question. By substituting these values, we get: $$OA\times OB=\left| \begin{matrix} i & j & k \\\ 1 & -2 & 1 \\\ -2 & 1 & 1 \\\ \end{matrix} \right|=-3\hat{i}-3\hat{j}-3\hat{k}=-3\left( i+j+k \right)$$ Similarly, we know AB, Ac lie on ABC plane. So, we can say AB x AC is the direction of normal. From question C is (+1, -1, 2). By above conditions, we get: $AB\times AC=\left| \begin{matrix} i & j & k \\\ -3 & 3 & 0 \\\ 0 & -1 & -1 \\\ \end{matrix} \right|=-3i-3j+3k=-3\left( i+j-k \right)$ Let the angle between the normal is X. By this we get: $\begin{aligned} & \cos X=\dfrac{-9\left( i+j+k \right)\left( i+j-k \right)}{{{\left( 3\sqrt{3} \right)}^{2}}} \\\ & =-\dfrac{1}{3} \\\ \end{aligned}$ We know the angle between planes is the angle between normal. So, by above equation after applying ${{\cos }^{-1}}$ , we get: $X={{\cos }^{-1}}\left( -\dfrac{1}{3} \right)$ So, the angle between planes is given by ${{\cos }^{-1}}\left( -\dfrac{1}{3} \right)$ Option(c) is correct. Note: The idea of angle between the normals is the same as the angle between planes is crucial. Try to think deep and prove it. The direction of normal of a plane is a cross product of any two lines on that plane. This idea is also crucial to understand. We can say this from Fleming’s left hand rule. The cross product of 2 vectors is always perpendicular to them.