Question
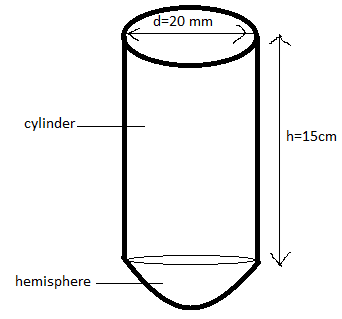
Question: A test tube has a diameter 20 mm and height is 15 cm. The lower portion is a hemisphere. Find the ca...
A test tube has a diameter 20 mm and height is 15 cm. The lower portion is a hemisphere. Find the capacity of the test tube. (π = 3.14)
Solution
Hint: Divide the test tube into a hemisphere and a cylinder. Find both the volumes and add them to find the capacity of the test tube. The capacity of the test tube is nothing but the volume of the test tube. Convert the measurements into the same units.
Complete step-by-step answer:
Given Data
Diameter d = 20 mm = 2 cm (1 cm = 10 mm)
Radius r = 10 mm = 1 cm (r = 2d)
Let us consider the volume of the cylinder as V1 and volume of the hemisphere as V2.
Volume of a cylinder = 2πrh (where r – radius and h – height)
And, Volume of hemisphere = 32πr3(where r – radius)
Now V1 = 2 × 3.14 × 1 × 15 = 94.2 cm3
V2 = 32×3.14×13=2.093cm3
Now volume of test tube = V1 + V2
⇒V = 94.2 + 2.093 = 96.293cm3
The capacity of is the volume of the test tube which is 96.293cm3
Note: The pivotal part of the problem is to break down the given figure into known figures with known formulae. In this problem the volume of the test tube is unknown but when it is broken down into a cylinder and a hemisphere whose volumes are known the problem becomes pretty straight forward.
