Question

A test three multiple choice questions that offer five possible answers. Draw a tree diagram that shows all the possible multiple-choice combinations for the answers to the test and determine the probability that a student will get two out of three questions correct by guessing on all of them: -
(a) $\dfrac{12}{125}$
(b) $\dfrac{16}{125}$
(c) $\dfrac{12}{145}$
(d) $\dfrac{16}{145}$

Answer 1

To solve this question, first we will find the total number of possible outcomes and then we will find those outcomes in which student will get two of three questions correct by guessing all of them. Then the probability will be obtained by dividing the number of possible outcomes by total number of outcomes.

Complete step-by-step answer:
Before starting to solve this question, we are going to draw a three diagram that will show all the possible multiple-choice combinations for the answers to the test:

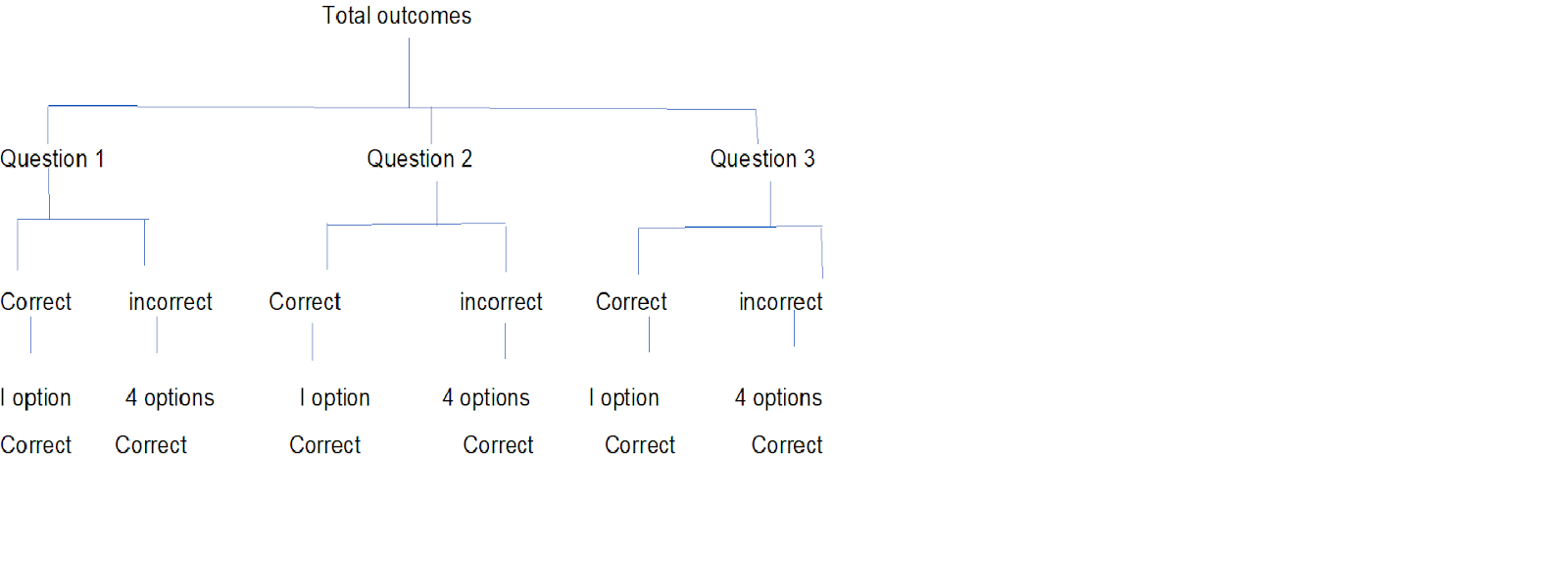
We know that there are five possible outcomes for each question, as there are five options (and we are assuming that only one of them is correct). Now there are three multiple choice questions. So, the total number of outcomes will be:
Total number of outcomes
$\begin{aligned} & 5\times 5\times 5 \\\ & =125 \\\ \end{aligned}$
Now, we have to consider that case only in which any two of three questions are correct. First we will select which of the two questions are correct. Now, we know that four out of 5 options only one is correct and the other four options are incorrect. The correct option in two questions will be correct only in one way. Now the third question is wrong so the number of ways of selecting the wrong option is $^{4}{{C}_{1}}=4$.
$\begin{aligned} & =3\times 1\times 1\times 4 \\\ & =12 \\\ \end{aligned}$
Now, we have to find the probability. Probability is given by:
$\begin{aligned} & probability=\dfrac{favourable\ outcomes}{total\,number\,of\,outcomes} \\\ & probability=\dfrac{12}{125} \\\ \end{aligned}$

So, the correct answer is “Option A”.

Note: The above question can also be solved by binomial distribution of probability. This method is as follow:
The probability of getting ‘r’ success in ‘n’ trials is given by:
$P\left( x=r \right){{=}^{\,n}}{{c}_{r}}\times {{p}^{r}}\times {{q}^{n-r}}$, where p= probability of success and q= probability of failure. N= total number of trials.