Question
Question: A test charge is moved without acceleration from A to C along the path from A to B and then from B t...
A test charge is moved without acceleration from A to C along the path from A to B and then from B to C in electric field E as shown in the figure.
(i) Calculate the potential difference between A and C.
(ii) At which point of the two is the electric potential more and why?
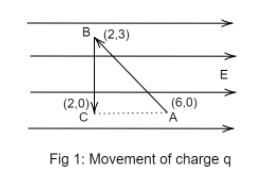
Solution
1. The potential difference doesn’t depend on the path taken to displace a charge from one point to another. Electric potential is produced by a conservative electric field. In any conservative field, only starting and endpoints matter to define potential not the path.
2. In the direction of the field, a point that is nearer to the source or located earlier along the field lines generally has a higher potential than other.
Formula used:
1. Two-point distance formula in 2D:d=(xfinal−xinitial)2+(yfinal−yinitial)2
Where, d is the distance between two points
And
2. Electric field
E=dx−dV ……(1)
where,
V is the potential.
x is the displacement.
Complete step by step solution:
Given:
The charge is displaced as in fig 1.
Electric field = E
We need to find the potential difference between A and C.
(i) Find the displacement of the charge:
Distance between point A and C=2−6
Distance between point A and C=−4
Rearrange eq (1) to get:
Edx=−dV
Integrate for the total displacement of the charge. As the potential doesn’t depend on the path taken, we can take the limits as VA and VC:
0∫xEdx=−VA∫VCdV
Put x=−4as the displacement from A to C:
⇒E(−4−0)=−(VC−VA)
⇒VC−VA=4E
(ii) We have seen in (i) that VC−VA is a positive quantity. This implies that VC>VA.
∴ (i) The potential difference between A and C is 4E.
(ii) The potential at point C is more than the potential at point A.
Note:
In questions like these, apply the right-hand thumb rule to find the direction of the induced magnetic field. Then apply Lenz’s law to find the induced current generated in the rings to oppose it.
