Question

A taxi leaves the station X for station Y every 10 minutes. Simultaneously, a taxi leaves station Y also for station X every 10 minutes. The taxis move at the same constant speed and go from X to Y or vice-versa in 2 hours. How many taxis coming from the other side will each taxi meet en route from Y to X ?
A. 10
B. 12
C. 11
D. 23

Answer 1

The problem is based on one’s understanding of the given condition. The most important rule that governs the problem is each taxi starting every 10 minutes. But, we must only consider the taxis starting at the other station, i.e. X. Consider the no. of taxis encountered in each hour and then add them up.

Complete answer:
Let us draw a simple sketch for a better understanding of the solution.

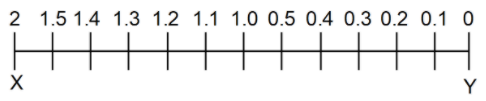
They’ve given in the question that each taxi leaves from the respective station every 10 minutes. And asked for how many taxis from X will one meet on its journey if they’re starting at Y.
If you consider the taxi that is starting at Y, there will be 12 taxis that have already started their journey from X to reach Y. So, it will meet these 12 taxis, while coming, halfway from Y i.e. in 1 hour.
Now, that the taxi is halfway from Y, there must be 6 taxis on the way from X. And another 5 taxis that start their journey in the 1 hour. Thus, a total of 11 taxis, in the next hour.
So, the total number of taxis one will encounter on its journey from Y to X will be the 12 taxis in the first hour and the 11 taxis in the second hour, which gives us a total of 23 taxis.

Therefore, the correct option is D.

Note:
The question is a little twisted, saying that the taxis are starting from both station X and station Y, simultaneously. But, as they asked for only the taxis coming from the other side, we don’t have to consider the taxis starting at Y. You can understand the problem better if you think of a two-lane and imagine how many you’ll encounter in the opposite lane.