Question

A taxi charge ${\text{Rs}}.20$ for the first $km$& @ ${\text{Rs}}{\text{.1}}2$ per $km$ for subsequent distance covered. Taking the distance as $x{\text{ }}km$ and a total fare ${\text{Rs}}{\text{. }}y$, write a linear equation depicting the relation in $x{\text{ and }}y$. From your graph find the taxi charges for covering ${\text{16 }}km$.

Answer 1

Hint: In this question, the linear equation is formed by equating the taxi charges and the distance covered multiplied with their respective charges. Then plot the graph for the obtained linear equation in two variables and then find the point at which the distance covered is ${\text{16 }}km$ to find the required taxi charges.

Complete step-by-step answer:
Given taxi charges for the first $km$ = ${\text{Rs}}.20$
Taxi charges for next subsequent distance in $km$ = ${\text{Rs}}{\text{.1}}2$
The total distance covered = $x{\text{ }}km$
The total fare = ${\text{Rs}}{\text{. }}y$
So, the total fare is given by
$\Rightarrow y = 20\left( {{\text{for first }}km} \right) + 12\left[ {\left( {{\text{total distance}} - 1} \right){\text{ in }}km} \right]$
By using the above data, we have

$$\Rightarrow y = 20 + 12\left( {x - 1} \right) \\\ \Rightarrow y = 20 + 12x - 12 \\\ \therefore y = 12x + 8 \\\$$

Thus, the linear equation depicting the relation in $x{\text{ and }}y$ is $y = 12x + 8$.
Drawing graph to the linear equation, by using the given below table, we have

For equation $y = 12x + 8$

$x$| - 2| - 1| 0| 1| 2
$y$| - 16| - 4| 8| 20| 32

So, the graph is shown below:

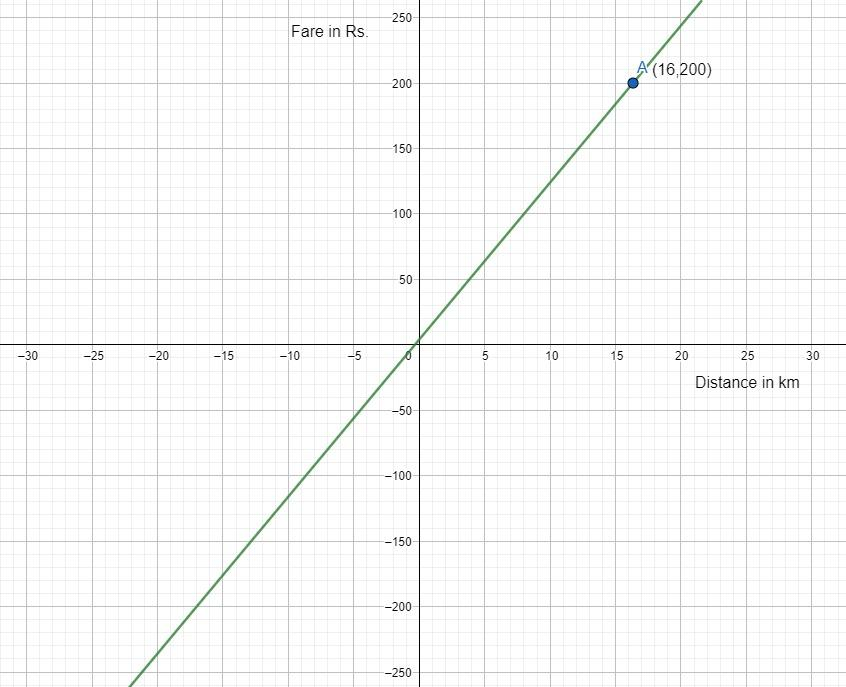
Now we have to plot the point at which the distance covered is $16{\text{ }}km$i.e., $x = 16$
So, clearly from the graph $y = 200$ when $x = 16$.
Therefore, the taxi charges are Rs. 200.

Note: The graph is taken on the bases of the scale 1 unit = $5{\text{ }}km$on x-axis at which distance is covered and 1 unit = ${\text{Rs}}.50$ on y-axis at which taxi charges are mentioned. The taxi charges cannot be negative as the distance covered is positive.