Question

A tank with rectangular base and rectangular sides open at top is to be contrasted so that its depth is 2m and volume is $8{m^3}$. If building a tank costs R.s. 70 per square metre for the base and R.s. 45 per square metre for sides, what is the cost of the least expensive tank?

Answer 1

Here we will proceed by calculating volume of tank and area of base. Then we will find the area of sides and use differentiation to find the length of sides. Hence we will find the least cost of a tank.

Complete step-by-step answer:

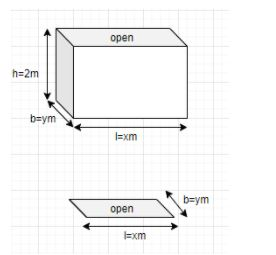
Firstly, given that the depth of the tank is 2m and the volume of the tank is $8{m^3}$.
Now x be the length and y be the breadth of tank.
Also we know that,
$\Rightarrow$ Volume of tank = $l \times b \times h$
$\Rightarrow 8 = 2 \times x \times y$
Or $4 = xy$
Or $y = \dfrac{4}{x}$
Also we are given that cost of building the tank R.s. 70 per square metre for base.
Volume of rectangular base = $l \times b$
Area of rectangular base = $xy$
Cost of rectangular base = $70\left( {xy} \right)$
Also we are given that cost is R.s. 45 per square metre for rectangular sides.
Area of rectangular sides = $2\left( {lh + hb} \right)$
$= 2\left( {2x + 2y} \right)$
$= 4\left( {x + y} \right)$
Cost of making rectangular sides = $45\left[ {4\left( {x + y} \right)} \right] = 180\left( {x + y} \right)$
Now we assume C as the total cost of tank
$\Rightarrow$ C(x) = cost of rectangular base + cost of rectangular sides
$\Rightarrow$ C(x) = 70(x y) +180(x + y)
Or $70\left( 4 \right) + 180\left( {x + \dfrac{4}{x}} \right)$
Or $280 + 180\left( {x + \dfrac{4}{x}} \right)$ [ from equation 1, $y = \dfrac{4}{x}$ ]
Or $280 + 180\left( {x + 4{x^{ - 1}}} \right)$
Now we need to minimize the cost of tank
We have to find $C'\left( x \right)$
Using $C'\left( x \right) = 280 + 180\left( {x + 4{x^{ - 1}}} \right)$
$\Rightarrow$We will now differentiate w.r.t. x
$\Rightarrow C'\left( x \right) = \dfrac{{d\left( {280 + 180\left( {x + 4{x^{ - 1}}} \right)} \right)}}{{dx}}$
Or $C'\left( x \right) = 0 + 180\left( {1 + \left( { - 1} \right)4{x^{ - 1 - 1}}} \right)$
Or $C'\left( x \right) = 180\left( {1 - \dfrac{4}{{{x^2}}}} \right)$
Putting $C'\left( x \right) = 0$
$\Rightarrow 180\left( {1 - \dfrac{4}{{{x^2}}}} \right) = 0$
Or $\left( {1 - \dfrac{4}{{{x^2}}}} \right) = 0$
Or $\dfrac{{\left( {{x^2} - 4} \right)}}{{{x^2}}} = 0$
Or $\left( {x - 2} \right)\left( {x + 2} \right) = 0$
So, x=2 or x=-2
We will take the length of the side as positive because length cannot be negative.
$\Rightarrow$ Finding $C''\left( x \right)$
$\Rightarrow C'\left( x \right) = 180\left( {1 - 4{x^{ - 2}}} \right)$
Differentiating w.r.t. x
$\Rightarrow C''\left( x \right) = \dfrac{{d\left( {180\left( {1 - 4{x^{ - 2}}} \right)} \right)}}{{dx}}$
Or $180\dfrac{{d\left( {1 - 4{x^{ - 2}}} \right)}}{{dx}}$
Or $180\left( {8{x^{ - 3}}} \right)$
Or $\dfrac{{1440}}{{{x^3}}}$
Putting x=2,
$C''(2) = \dfrac{{1440}}{{{{\left( 2 \right)}^3}}}$ >0
$\Rightarrow$ x=2 is point of minima
$\Rightarrow$ $C'\left( x \right)$ is least at x=2
Thus,
Least cost of construction
$C'\left( x \right) = 280 + 180\left( {2 + \dfrac{4}{2}} \right)$
= $280 + 180\left( {2 + 2} \right)$
= 280 + 720
= 1000
Hence, the least cost of construction is R.s. 1000.

Note: In this type of question, one can get confused to find the cost of a tank. So we must concentrate that cost should include both the cost of base and cost of sides. Also we should take the length as positive not negative. Hence we will get the desired result.