Question

A tank, which is open at the top, contains a liquid up to a height $H$ . A small hole is made in the side of a tank at a distance $y$ below the liquid surface. The liquid emerging from the hole lands at a distance $x$ from the tank.

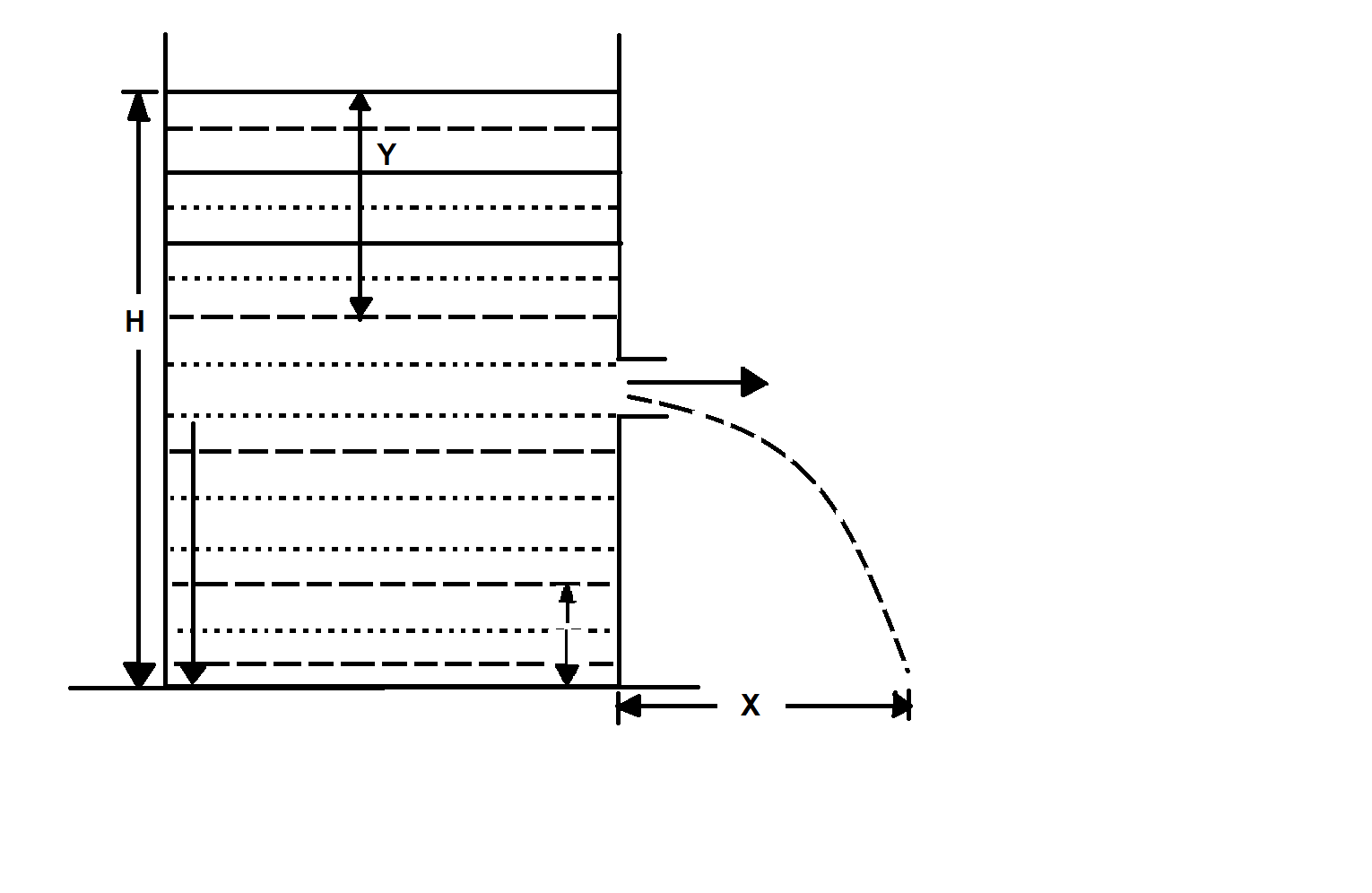
$\left( a \right)$ If $y$ is increased from zero to$H$ . $x$ will first increase and then decrease.
$\left( b \right)$ $x$ is maximum for $y = \dfrac{H}{2}$ .
$\left( c \right)$ The maximum value of $x$ is$H$ .
$\left( d \right)$ The maximum value of $x$ will depend on the density of the liquid.

Answer 1

We are given with the level markings on the tank and are asked to find the change in basically the value $x$ as $y$ changes. Thus, we will take into account the efflux velocity of the liquid flowing out. Then, we will differentiate it with respect to the targeted variable.
Formulae Used:
$v = \sqrt {2gy}$
Where, $v$ is the efflux velocity, $g$ is the acceleration due to gravity and $y$ is the reduced height of the liquid.

Complete Step by Step Solution:
Here,
The liquid coming out of the opening is a parabola.
Clearly,
The emerging liquid moves upwards as the projectile reaches the ground after time $t$ .
Thus,
We have
$\Rightarrow H - y = \dfrac{1}{2}g{t^2}$
Thus,
Targeting the time and rearranging the equation, we get
$\Rightarrow t = \sqrt {\dfrac{{2(H - y)}}{g}}$
Thus,
We can say,
$x = vt$
Substituting the values, we get
$\Rightarrow x = \sqrt {2gy} \times \sqrt {\dfrac{{2(H - y)}}{g}}$
Further, we can say
$\Rightarrow x = 2\sqrt {(H - y)y}$
Now,
Differentiating both sides with respect to $y$ , we get
$\Rightarrow \dfrac{{dx}}{{dy}} = \dfrac{{(H - 2y)}}{{\sqrt {(H - y)y} }}$
Now,
Clearly,
$\Rightarrow \dfrac{{dx}}{{dy}} > 0$ If $y < \dfrac{H}{2}$
And,
$\Rightarrow \dfrac{{dx}}{{dy}} < 0$ If $y > \dfrac{H}{2}$
Thus, option $\left( a \right)$ is correct.
Also,
For maxima or minima,
$\Rightarrow \dfrac{{dx}}{{dy}} = 0$
Thus, we can say
$\Rightarrow H - 2y = 0$
That means,
$\Rightarrow y = \dfrac{H}{2}$
Hence, the option $\left( b \right)$ is also correct.
Now,
The maximum value of $x$ is at $y = \dfrac{H}{2}$.
Thus,
$\Rightarrow {x_{\max }} = 2\sqrt {(H - \dfrac{H}{2}) \times \dfrac{H}{2}}$
Thus, we get
$\Rightarrow {x_{\max }} = H$
Hence, the option $\left( c \right)$ is also correct.
Now,

Option $\left( d \right)$ is clearly incorrect as the efflux itself is independent of the density of the liquid. Thus, it is not possible to have $x$ depending on the density of the liquid.

Note: As we have seen here, a question can have more than one correct answer. So, it is better to go through a generalized methodology to solve a problem otherwise we might end up overlooking the multiple correct possibility. We can also make a habit of cross checking all the given options before we finalize.