Question

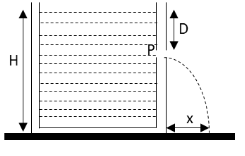
A tank is filled with water up to a height $H$. Water is let out of hole P from one of the walls, at a depth $D$ below the surface of water. Express the range of efflux in terms of $H$ and $D$.

Answer 1

Use the formula for kinetic energy and potential energy of an object. Apply law of conservation of energy to the upper water surface and at the point P to calculate the velocity of the water coming out of the hole. Use a kinematic equation for displacement of an object to calculate the time required for the water from the hole to reach the ground. Use the formula for velocity and calculate the range of the efflux.

Formulae used:
The kinetic energy $K$ of an object is
$K = \dfrac{1}{2}m{v^2}$ …… (1)
Here, $m$ is the mass of the object and $v$ is the velocity of the object.
The potential energy $U$ of an object is
$U = mgh$ ……. (2)
Here, $m$ is the mass of the object, $g$ is acceleration due to gravity and $h$ is the height of the object from the ground.
The kinematic equation for displacement $s$ of an object is
$s = ut + \dfrac{1}{2}a{t^2}$ …… (3)
Here, $u$ is initial velocity of the object, $t$ is time and $a$ is acceleration of the object.
The velocity $v$ of an object is
$v = \dfrac{s}{t}$ …… (4)
Here, $s$ is the displacement of the object and $t$ is the time.

Complete step by step answer:
We have given that the height of the water level in a tank is $H$ and the distance of the hole P in one of the walls of the tank is at a distance $D$ from the upper surface of the water.The distance at which the water falls after emitting from the hole P is $x$.We are asked to calculate this distance $x$ in terms of $H$ and $D$.

Let us first calculate the horizontal velocity of the water coming out of the hole at point P.According to the law of conservation of energy, the potential energy ${U_u}$ of the water at the upper surface of the tank is equal to the kinetic energy ${K_P}$ of the water coming out of the hole.
${U_u} = {K_P}$
$\Rightarrow mgD = \dfrac{1}{2}m{v^2}$
$\Rightarrow v = \sqrt {2gD}$
This is the expression for horizontal velocity of the water coming out of the hole.

The vertical component of the velocity of water coming out of the hole is zero.
${u_y} = 0\,{\text{m/s}}$
Rewrite equation (3) for the vertical displacement of the water from the hole P to the ground.
$H - D = \left( {0\,{\text{m/s}}} \right)t + \dfrac{1}{2}g{t^2}$
$\Rightarrow H - D = \dfrac{1}{2}g{t^2}$
$\Rightarrow t = \sqrt {\dfrac{{2\left( {H - D} \right)}}{g}}$
This expression gives the expression for the time required for the water from the whole to reach the ground.

Let us not calculate the horizontal range of the water.
Substitute $x$ for $s$ in equation (4).
$v = \dfrac{x}{t}$
$\Rightarrow x = vt$
Substitute $\sqrt {2gD}$ for $v$ and $\sqrt {\dfrac{{2\left( {H - D} \right)}}{g}}$ for $t$ in the above equation.
$\Rightarrow x = \sqrt {2gD} \sqrt {\dfrac{{2\left( {H - D} \right)}}{g}}$
$\therefore x = \sqrt {D\left( {H - D} \right)}$

Hence, the range of the water is $\sqrt {D\left( {H - D} \right)}$.

Note: The students may think that in the kinematic equation for vertical displacement of the water we have not used the acceleration due to gravity with negative sign. But the students should keep in mind that the vertical displacement of the water is also in the downward direction. Hence, the negative sign of the acceleration due to gravity and vertical displacement of water cancel each other.