Question

A tank is filled by liquid of density $\rho$up to height H. The average pressure on the walls of container is:
A. $\rho gH$
B. $\dfrac{1}{2}\rho gH$
C. $\dfrac{1}{4}\rho gH$
D. $\dfrac{1}{8}\rho gH$

Answer 1

Pressure is defined as the force exerted per area given as $P = FA$

In the case of columns of liquid of height H and density $\rho$pressure equation is given as $P = \rho gH$ where g is the gravitational acceleration.

In this question average pressure on the walls of the container now if we find the pressure for a small height of container and if we add the pressure for small height together we can find the pressure on full container.

Complete step by step answer:

Density of the liquid $\rho$
Height of the liquid H

We know
Pressure$P = \rho gH$

As the container is filled with the liquid up to the height H then the force on the walls by the liquid must be uniform throughout up to a height H, since the force is uniform let us find the force by liquid for a small area $dA$

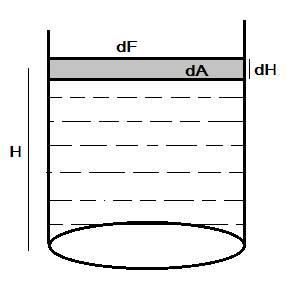
Therefore force on small $dA$area will be
$dF = P.dA - - (i)$,

Where $P = \rho gH$and$dA = 2\pi dH$, hence we can write equation (i) as
$dF = \left( {\rho gH} \right)\left( {2\pi dH} \right) - - (ii)$

Since we have got the force on the wall for a small area$dA$, now let us find the force on wall up to height 0 to H by integrating equation (ii),

$$\int\limits_0^F {dF} = \left( {\rho g} \right)2\pi \int\limits_0^H {HdH} \\\ \left[ F \right]_0^F = \left( {\rho g} \right)2\pi \left[ {\dfrac{{{H^2}}}{2}} \right]_0^H \\\ \left( {F - 0} \right) = \pi \rho g\left( {{H^2} - 0} \right) \\\ F = \pi \rho g{H^2} - - (iii) \\\$$

Since the average pressure is formulated as
Average pressure$P = \dfrac{F}{A} - - (iv)$

Now by substitute the value of force from equation (iv) and the area of the tank we get

$$P = \dfrac{F}{A} \\\ = \dfrac{{\pi \rho g{H^2}}}{{2\pi H}} \\\ = \dfrac{{\rho gH}}{2} \\\$$

Hence the average pressure on the walls of container is $= \dfrac{{\rho gH}}{2}$
Option B is correct

Note: Students must know that if we are asked to find the pressure on any uniform container we can find it by finding the pressure for a small area and then adding them together.