Question

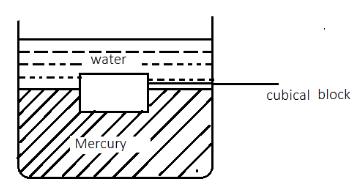
A tank contains water of mercury as shown in the figure. A cubical block of side 10cm is in equilibrium inside (Relative density of the material of block $= 7.2$ , relative density of mercury $= 13.6$ ).Find the height of the block above the mercury level.

\left( A \right)6cm \\\ \left( B \right)4.7cm \\\ \left( C \right)7cm \\\ \left( D \right)8cm \\\

Answer 1

Hint : In order to solve this question, we are going to consider the case in which the block will float above the mercury level and the condition for it. After that the weight of the mercury displaced by the block is found and is then compared with the weight of the iron block, which gives us the height.
The iron block floats, if
$weight\,of\,mercury\,displaced\, = \,weight\,of\,the\,iron\,block$

Complete Step By Step Answer:
From the information given in the question, we can see that the cubical block will float on mercury if the weight of the block is equal to the weight of the mercury displaced by it.
As it is given that the density of iron is, ${\rho _i} = 7.2gc{m^{ - 3}}$
While that of the mercury, ${\rho _m} = 13.6gc{m^{ - 3}}$
Now, length of each side of iron block is $= 10cm$
Let us consider that height of block above mercury in vessel is $h\,cm$
Then, volume of block inside mercury is,
$\Rightarrow {V_m} = 10 \times 10 \times \left( {10 - x} \right)$
This is the same as the volume of the mercury displaced by the block.
Weight equivalent to this volume of mercury is
$W = V{\rho _{ig}}$
Putting values, we get
$W = V \times 7.2 \times 981$
Then, the iron block floats
$weight\,of\,mercury\,displaced\, = \,weight\,of\,the\,iron\,block \\\ \Rightarrow 100 \times \left( {10 - x} \right) \times 13.6 \times 981 = 1000 \times 7.2 \times 981 \\\ \Rightarrow 100 \times \left( {10 - x} \right) \times 13.6 = 1000 \times 7.2 \\\ \Rightarrow \left( {10 - x} \right) \times 1360 = 7200 \\\ \Rightarrow 10 - x = \dfrac{{7200}}{{1360}} \\\ \Rightarrow x = 10 - 5.29 = 4.71$
Thus, the height of the block over the mercury level is $4.71cm$
Hence, option $\left( B \right)4.7cm$ is the correct answer.

Note :
For an object to float over some liquid’s surface it is necessary that the weight of the liquid displaced by it is equal to its own weight. Now if we are given with the density and the volume, weights can be measured and the dimensions of volume also give the idea of the height of water displaced.