Question

A tank containing water has an orifice on one vertical wall. If the center of the orifice is $4.9m$ below the surface of the water in the tank, the velocity of discharge is,
A. $0.98m/s$
B. $9.8m/s$
C. $98m/s$
D. $9.8cm/s$

Answer 1

The water tank has one orifice in $4.9m$. Due to gravity and pressure, the water will be forcibly come out from the orifice. Torricelli is one of the scientists who derived the equation of motion for this system. So we can use Torricelli’s Law to find the velocity of the discharged water.

Formula used:
$v = \sqrt {2gh}$
$v$ – Velocity of the discharged water
$g$ – Acceleration due to gravity ( $9.8m/s$ )
$h$ – Liquid height over reference point

Complete step by step solution:

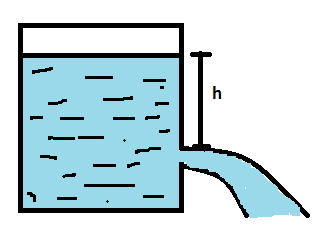
The liquid height over the reference point is represented as $h$, the value of $h$ is $4.9m$ and $g = 9.8m/s$.
From Torricelli’s law,
$v = \sqrt {2gh}$
$v = \sqrt {2 \times 9.8 \times 4.9}$m/s
$v = \sqrt {96.04}$m/s
$v = 9.8m/s$

Note:
Torricelli’s law explains the relationship between leaving liquid from the hole and the liquid’s height. The container is filled with water and it has a small hole at the bottom of the container. If the liquid starts to drop from a height$h$, it would leave from the hole with some velocity $v$. One of the scientists Evangelista Torricelli finds this relation.
If the system has the same level of water in the tank, the water didn’t come out so the velocity of the water from the orifice is zero. Torricelli law has practical applications in daily life.