Question
Question: A tangential force \( F \) acts at the top of a thin spherical shell of mass \( m \) and radius \( R...
A tangential force F acts at the top of a thin spherical shell of mass m and radius R . Find the acceleration of the shell if it rolls without slipping.
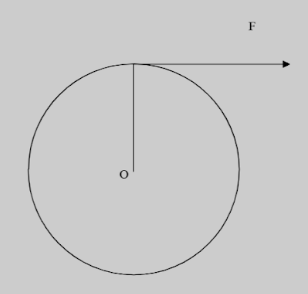
(A) 5m6F
(B) 5F6m
(C) 5F3m
(D) 6F5m
Solution
For the body to roll without slipping on the surface, the body would experience two different motions. Along the centre of mass, with linear velocity and around its centre, with angular velocity, and the linear velocity of the body would be v=ωR .
Formulas used: We would be using the formula a=αR where a is the linear acceleration along the centre of mass of the body experiencing rolling motion, α is the angular acceleration along the point of contact of the body experiencing rolling motion and R is the radius of the spherical shell.
We would also be substituting the moment of inertia of a sphere which is, I=32MR2 where M is the mass of the spherical body. We would also be using the formula to find the torque of a body, τ=Iα
Complete Step by Step answer
Let us consider the linear motion along the centre of mass of the body at first, which can be given by, F−f=Ma where f is the frictional force that the spherical shell might experience on it at the point of contact.
Considering the rotational motion, we can see that a torque develops at the point of contact which can be given by, τ=FR+fR=Iα . We also know that for rolling motion, α=Ra . Substituting the value of α for a body experiencing rolling motion, in the equation we get,
(F+f)R=IRa⇒(F+f)=IR2a .
Adding the two equations we get,
2F=IR2a+Ma
Also, we know that the moment of inertia of a spherical shell is I=32MR2
2F=(32MR2×R21+M)a
Solving for F we get,
2F=(32M+M)a=(35M)a
Now Solving to find acceleration of the body we get,
5Ma=6F
⇒a=5M6F
Hence the correct answer will be option A.
Note
While calculating rolling motion of a body in any plane we will have to evaluate equations for both rotational motion and linear motion such that the rotational motion is calculated along the point of contact of the body with the surface that causes friction, while linear motion is calculated along the centre of mass of the body.
