Question
Question: A tangential force acting on the top of the sphere of mass \(m\) kept on a rough horizontal place as...
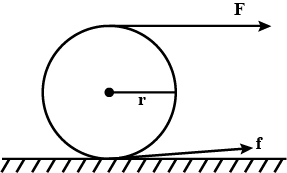
A tangential force acting on the top of the sphere of mass m kept on a rough horizontal place as shown in figure.
If the sphere rolls without slipping, then the acceleration with which the centre of sphere moves, is
A.7m10F
B.2mF
C.7m3F
D.2m7F
Solution
To solve this problem, firstly we will learn about Acceleration and the Angular Acceleration and by using the concept behind them (including all the required information). We will then calculate our solution by inserting the values of our formula. Hence, by this we can easily approach our answer.
Complete answer:
Acceleration is a vector quantity. It is defined as the rate by which a change of velocity occurs with the change in time. An object is accelerating if there is a change in velocity.
Angular Acceleration: Angular Acceleration is the rate of change of angular velocity with respect to time of an object in motion. It is the revision in velocity of moving an object with respect to time. If any object moves in a circular direction then its velocity is called angular velocity.
The rotational acceleration is the other name for Angular Acceleration. It is a quantitative declaration of the change in angular velocity per unit time. The acceleration vector, magnitude or length is ∝ to the rate of change in angular velocity.
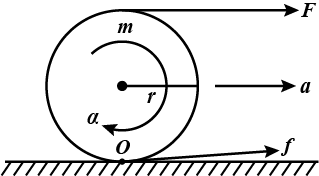
Assume, the angular acceleration of the sphere be α
Moment of inertia of the sphere, I=52mr2
Using: τ=Iα
∴(F−f)r=52mr2α ⇒α=2mr5(F−f).......................(1)
Acceleration of its center, a=mF+f.........................(2)
Acceleration of the point O is zero
i.e.a=ra ∴mF+f=r2mr5(F−f) or,2F+2f=5F−5f ⇒f=73F
Thus from (2) we get a=mF+73F=7m10F
So, the correct answer to this problem is option A.
Note: The Rotational acceleration is the other name for Angular acceleration, It is a quantitative expression of the change in angular velocity that a spinning object undergoes per unit time. It is a vector quantity, having both magnitude components and either of two defined directions.
