Question

A tangent to the parabola${{y}^{2}}=4ax$meets the axes at A and B. The locus of midpoint of AB is:
a) ${{y}^{2}}+2ax=0$
b) ${{y}^{2}}-2ax=0$
c) ${{y}^{2}}+ax=0$
d) $2{{y}^{2}}+ax=0$

Answer 1

Hint: Write the equation of the tangent on the parabola ${{y}^{2}}=4ax$ at a parametric point $\left( a{{t}^{2}},2at \right)$ .Then find the points on x and y axis where this tangent is intersecting. The intersecting points will be A and B then find the midpoint of A and B.

Complete step-by-step answer:
Let us take a parametric point $\left( a{{t}^{2}},2at \right)$ which lie on the parabola ${{y}^{2}}=4ax$ then we are going to write the equation of a tangent at this parametric point.
The slope of the tangent of the parabola ${{y}^{2}}=4ax$ is calculated below:
${{y}^{2}}=4ax$
Taking derivative with respect to x on both the sides will get:
$\begin{aligned} & 2y\dfrac{dy}{dx}=4a \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{2a}{y} \\\ \end{aligned}$
Now, substituting the parametric point $\left( a{{t}^{2}},2at \right)$ in the above equation we get the slope as:
$\begin{aligned} & \dfrac{dy}{dx}=\left( \dfrac{2a}{2at} \right) \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{1}{t} \\\ \end{aligned}$
The equation of a tangent at the parametric point with the slope $\dfrac{1}{t}$ is:
$y-2at=\dfrac{1}{t}\left( x-a{{t}^{2}} \right)$
When the above equation cut x axis then y = 0 and the coordinate of x is:
$\begin{aligned} & 0-2at=\dfrac{1}{t}\left( x-a{{t}^{2}} \right) \\\ & \Rightarrow -2a{{t}^{2}}=x-a{{t}^{2}} \\\ & \Rightarrow x=-a{{t}^{2}} \\\ \end{aligned}$
When the above equation cut y axis then x = 0 and the coordinate of y is:
$\begin{aligned} & y-2at=\dfrac{1}{t}\left( 0-a{{t}^{2}} \right) \\\ & \Rightarrow y=2at-at \\\ & \Rightarrow y=at \\\ \end{aligned}$
From the above calculations, coordinates of $A\left( -a{{t}^{2}},0 \right)$ and $B\left( 0,at \right)$ .
What we have described above is shown through the below diagram:

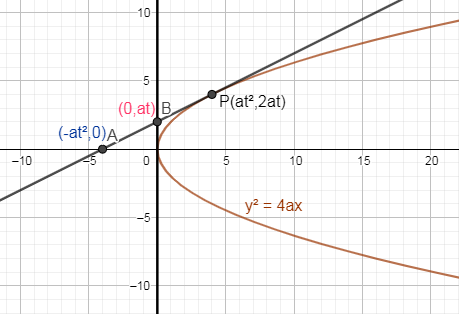
In the above figure, you can see a parabola ${{y}^{2}}=4ax$ on which a tangent is drawn at point $P\left( a{{t}^{2}},2at \right)$ and the tangent intersects X and Y axis at $A\left( -a{{t}^{2}},0 \right)$ and $B\left( 0,at \right)$ respectively.
The x and y coordinates of the midpoint of A and B is equal to:
$\left( -\dfrac{a{{t}^{2}}}{2},\dfrac{at}{2} \right)$
So, from the above expression $x=-\dfrac{a{{t}^{2}}}{2}$ and $y=\dfrac{at}{2}$ .
$y=\dfrac{at}{2}$
Squaring both the sides will give:
$\begin{aligned} & {{y}^{2}}=\dfrac{{{a}^{2}}{{t}^{2}}}{4} \\\ & \Rightarrow 4{{y}^{2}}={{a}^{2}}{{t}^{2}} \\\ & \Rightarrow {{t}^{2}}=\dfrac{4{{y}^{2}}}{{{a}^{2}}} \\\ \end{aligned}$
Substituting the value of ${{t}^{2}}$ in $x=-\dfrac{a{{t}^{2}}}{2}$ we get,
$\begin{aligned} & x=-\dfrac{a\left( \dfrac{4{{y}^{2}}}{{{a}^{2}}} \right)}{2} \\\ & \Rightarrow -2ax=4{{y}^{2}} \\\ & \Rightarrow 2{{y}^{2}}+ax=0 \\\ \end{aligned}$
Hence, the locus of the midpoint of A and B is $2{{y}^{2}}+ax=0$ .
Hence, the correct option is (d).

Note: The locus of a point is a relation between x and y which is holding one or more conditions like we have to find the locus of a midpoint of A and B.