Question

A tangent to the parabola ${{x}^{2}}+4ay=0$ cuts the parabola ${{x}^{2}}=4by$, at A and B the locus of the midpoint of AB is
(a) $\left( a+2b \right){{x}^{2}}=4{{b}^{2}}y$
(b) $\left( b+2a \right){{x}^{2}}=4{{b}^{2}}y$
(c) $\left( a+2b \right){{y}^{2}}=4{{b}^{2}}x$
(d) $\left( b+2a \right){{x}^{2}}=4{{a}^{2}}y$

Answer 1

Hint: Write equation of tangent on the parabola ${{x}^{2}}+4ay=0$. And find the intersection of tangent and the parabola ${{x}^{2}}=4by$. Don’t calculate the exact coordinates. Try to use the equation to get locus of the mid-points of A and B.

Complete step-by-step answer:
Let us suppose a parametric coordinate on parabola ${{x}^{2}}+4ay=0$ as $\left( 2at,-a{{t}^{2}} \right)$.
Now, we can write the equation of tangent through this point by T=0.
If $\left( {{x}_{1,}}{{y}_{1}} \right)$is a point on parabola, ${{x}^{2}}=-4ay$, then tangent through it is given as
$x{{x}_{1}}=-4a\dfrac{\left( y+{{y}_{1}} \right)}{2}=-2a\left( y+{{y}_{1}} \right)$

As, we have points $\left( {{x}_{1,}}{{y}_{1}} \right)$ as $\left( 2at,-a{{t}^{2}} \right)$.
Hence tangent through it be
$\begin{aligned} & x\left( 2at \right)=-2a\left( y+\left( -a{{t}^{2}} \right) \right) \\\ & \Rightarrow 2atx=-2a\left( y-a{{t}^{2}} \right) \\\ & \Rightarrow atx+ay-{{a}^{2}}{{t}^{2}}=0 \\\ & \Rightarrow tx+y-a{{t}^{2}}=0............(i) \\\ \end{aligned}$

Now, let us suppose, tangent is intersecting the parabola ${{x}^{2}}=4by$ at points $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{x}},{{y}_{2}} \right)$ and mid-point of them as (h,k).

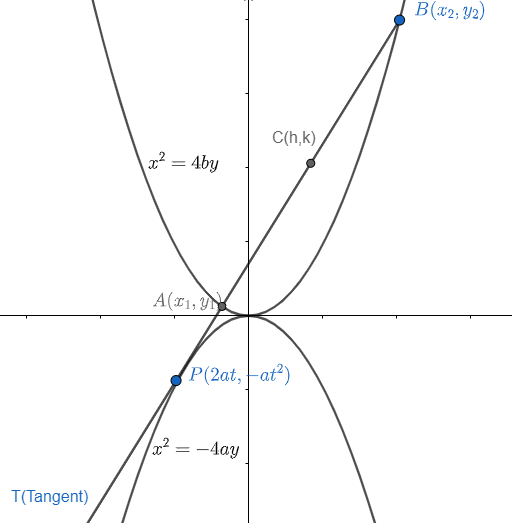
Let us find the intersection points of parabola ${{x}^{2}}=4by$ and the tangent ‘T’ on ${{x}^{2}}=-4ay$.
So, from equation ${{x}^{2}}=4by$, we get
$y=\dfrac{{{x}^{2}}}{4b}$ ………………….. (ii)
Putting value of ‘y’ from equation (ii) in equation (i), we get
$\begin{aligned} & tx+\dfrac{{{x}^{2}}}{4b}-a{{t}^{2}}=0 \\\ & \Rightarrow {{x}^{2}}+4btx-4ab{{t}^{2}}=0..........(iii) \\\ \end{aligned}$

As above equation is a quadratic equation so, we can get values of $\left( {{x}_{1}},{{x}_{2}} \right)$ as roots of equation (iii).
Now, we know the relation of roots with the coefficients of quadratic equation which is given as
$\text{sum of roots = - }\dfrac{\text{coefficient of x}}{\text{coefficient of }{{\text{x}}^{\text{2}}}}$ ……….. (iv)
$\text{product of roots = }\dfrac{\text{constant term}}{\text{coefficient of }{{\text{x}}^{\text{2}}}}$ ……………. (v)

Now, from equation (iii), (iv) and (v), we get
${{x}_{1}}+{{x}_{2}}=-4bt$ ………………. (vi)
${{x}_{2}}+{{x}_{2}}=4ab{{t}^{2}}$ ……………… (vii)
Similarly, we can get a quadratic in ‘y’ if we put value of ‘x’ from equation of tangent i.e. $tx+y-a{{t}^{2}}=0$ in equation of parabola ${{x}^{2}}=4by$. Hence, we get
${{\left( \dfrac{a{{t}^{2}}-y}{t} \right)}^{2}}=4by$
Now, use ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ , we get
$\begin{aligned} & \dfrac{{{a}^{2}}{{t}^{4}}+{{y}^{2}}-2ay{{t}^{2}}}{{{t}^{2}}}=4by \\\ & \Rightarrow {{y}^{2}}-2a{{t}^{2}}y-4b{{t}^{2}}y+{{a}^{2}}{{t}^{4}}=0 \\\ & \Rightarrow {{y}^{2}}-\left( 2a{{t}^{2}}+4b{{t}^{2}} \right)y+{{a}^{2}}+{{t}^{4}}=0.......(viii) \\\ \end{aligned}$

Now, ${{y}_{1}}$ and ${{y}_{2}}$ are roots of above equation hence from equation (iv) and (v), we get
${{y}_{1}}+{{y}_{2}}=2a{{t}^{2}}+4b{{t}^{2}}$ …………….. (ix)
${{y}_{1}}{{y}_{2}}={{a}^{2}}{{t}^{4}}$……………. (x)
Now, as we need to find locus of midpoint of AB which can be given as
$h=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ and $k=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$
Hence, from equation (vi) and (ix), we get
$h=\dfrac{-4bt}{2}$ and $k=\dfrac{2a{{t}^{2}}+4b{{t}^{2}}}{2}$
H=-2bt and $k=\dfrac{2a{{t}^{2}}}{2}+\dfrac{4b{{t}^{2}}}{2}=a{{t}^{2}}+2b{{t}^{2}}$

Now, we can eliminate ‘t’ by substituting value of ‘t’ from relation h and t to relation ‘k’ and ’t’, hence, we get so, we have
$t=\dfrac{-h}{2b}$
And hence
$\begin{aligned} & k=a{{\left( \dfrac{-h}{2b} \right)}^{2}}+2b{{\left( \dfrac{-h}{2b} \right)}^{2}} \\\ & k=\dfrac{{{h}^{2}}a}{4{{b}^{2}}}+\dfrac{2b{{h}^{2}}}{4{{b}^{2}}} \\\ \end{aligned}$

Now, replacing (h, k) by (x, y) to get the required locus. Hence, we get
$\begin{aligned} & y=\dfrac{{{x}^{2}}a}{4{{b}^{2}}}+\dfrac{2b{{x}^{2}}}{4{{b}^{2}}} \\\ & 4{{b}^{2}}y={{x}^{2}}\left( a+2b \right) \\\ \end{aligned}$

Hence, option (a) is the correct answer.

Note: Another approach for the given problem would be that we can suppose parametric coordinates of points A and B lying on ${{x}^{2}}=4by$. And write the equation of line passing through A and B. Now, this line is acting as a tangent for ${{x}^{2}}=-4ay$. So, intersection of them would be the only point. So, use this condition to get equations in parametric variables and hence get locus of midpoint of A and B.
One can suppose parametric coordinates at ${{x}^{2}}=-4ay$ as $\left( -2at,-a{{t}^{2}} \right)$as well.
Calculation is the important side of the problem as well. So, take care of it.
Writing tangent equation through point $\left( {{x}_{1}},{{y}_{1}} \right)$ on any curve f(x)=0 is given by replacing
$\begin{aligned} & {{\text{x}}^{\text{2}}}\text{ by x}{{\text{x}}_{\text{1}}} \\\ & {{\text{y}}^{\text{2}}}\text{ by y}{{\text{y}}_{\text{1}}} \\\ & \text{x by }\dfrac{\text{x+}{{\text{x}}_{\text{1}}}}{\text{2}} \\\ & \text{y by }\dfrac{\text{y+}{{\text{y}}_{\text{1}}}}{\text{2}} \\\ \end{aligned}$