Question

A tangent to the hyperbola ${{x}^{2}}-2{{y}^{2}}=4$ meets x – axis at P and y – axis at Q. Line PR and QR are drawn such that OPRQ is a rectangle (where O is the origin). The locus of R is?
(a) $\dfrac{4}{{{x}^{2}}}+\dfrac{2}{{{y}^{2}}}=1$
(b) $\dfrac{4}{{{x}^{2}}}-\dfrac{2}{{{y}^{2}}}=1$
(c) $\dfrac{2}{{{x}^{2}}}+\dfrac{4}{{{y}^{2}}}=1$
(d) $\dfrac{2}{{{x}^{2}}}-\dfrac{4}{{{y}^{2}}}=1$

Answer 1

In the equation of the hyperbola given divide both the sides with 4 and write it in the standard form given as $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. Now, assume the point at which the tangent is as $M\left( a\sec \theta ,b\tan \theta \right)$. Find the slope of this tangent line at point M by differentiating the equation of the hyperbola and substituting the values of x and y coordinates. Now, assume the coordinates of point R as (h, k). Find the point at which the tangent line cut the x and y axis to get the values of h and k respectively. Find the relation between h and k by eliminating all other variables and finally substitute x in place of h and y in place of k to get the required locus.

Complete step-by-step answer:
Here we have been provided with the hyperbola ${{x}^{2}}-2{{y}^{2}}=4$ whose tangent at a point meets the x and y axis at P and Q respectively. OPRQ is a rectangle and we are asked to find the locus of point R.
Now, the equation of hyperbola is ${{x}^{2}}-2{{y}^{2}}=4$ so let us convert it into the standard form given as $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. Dividing both the sides with 4 in the given equation we get,
$\begin{aligned} & \Rightarrow \dfrac{{{x}^{2}}}{4}-\dfrac{{{y}^{2}}}{2}=1 \\\ & \Rightarrow \dfrac{{{x}^{2}}}{{{2}^{2}}}-\dfrac{{{y}^{2}}}{{{\left( \sqrt{2} \right)}^{2}}}=1 \\\ \end{aligned}$
Now, we know that any point on the hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is assumed as $\left( a\sec \theta ,b\tan \theta \right)$, so let us assume that the tangent is drawn on the hyperbola $\dfrac{{{x}^{2}}}{{{2}^{2}}}-\dfrac{{{y}^{2}}}{{{\left( \sqrt{2} \right)}^{2}}}=1$ at point $M\left( 2\sec \theta ,\sqrt{2}\tan \theta \right)$. Let us draw a diagram of the given situation.

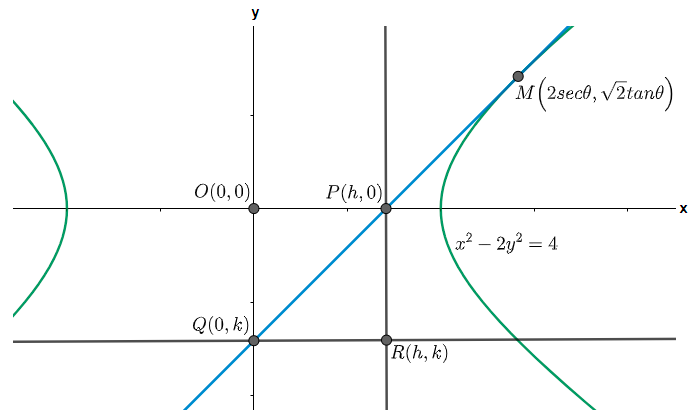
In the above diagram OPRQ is a rectangle and we have assumed the coordinates of the point R as (h, k). Using the property of rectangle we can say that the coordinates of point P will be (h, 0) and that of Q will be (0, k). We need to find the values of h and k.
Now, the slope of tangent at point M on the hyperbola can be obtained by differentiating the equation and substituting the values of x and y coordinates. So we get,
$\begin{aligned} & \Rightarrow \frac{d\left( {{x}^{2}}-2{{y}^{2}} \right)}{dx}=\frac{d\left( 4 \right)}{dx} \\\ & \Rightarrow 2x-2\times 2y\frac{dy}{dx}=0 \\\ & \Rightarrow \frac{dy}{dx}=\frac{x}{2y} \\\ \end{aligned}$
Substituting the values of x and y we get,
$\begin{aligned} & \Rightarrow \dfrac{dy}{dx}=\dfrac{2\sec \theta }{2\sqrt{2}\tan \theta } \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{1}{\sqrt{2}\sin \theta } \\\ \end{aligned}$ $\Rightarrow \dfrac{dy}{dx}=\dfrac{{}}{2y}$
So the equation of the tangent can be given by the point slope form of the line $\left( y-{{y}_{1}} \right)=\dfrac{dy}{dx}\left( x-{{x}_{1}} \right)$ where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the point through which the line is passing, therefore we have,
$\begin{aligned} & \Rightarrow \left( y-\sqrt{2}\tan \theta \right)=\dfrac{1}{\sqrt{2}\sin \theta }\left( x-2\sec \theta \right) \\\ & \Rightarrow y=\dfrac{x}{\sqrt{2}\sin \theta }-\dfrac{\sqrt{2}}{\sin \theta \cos \theta }+\dfrac{\sqrt{2}\sin \theta }{\cos \theta } \\\ & \Rightarrow y=\dfrac{x}{\sqrt{2}\sin \theta }-\dfrac{\sqrt{2}}{\sin \theta \cos \theta }\left( 1-{{\sin }^{2}}\theta \right) \\\ \end{aligned}$
Using the trigonometric identity ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$ we get,
$\begin{aligned} & \Rightarrow y=\dfrac{x}{\sqrt{2}\sin \theta }-\dfrac{\sqrt{2}}{\sin \theta \cos \theta }\left( {{\cos }^{2}}\theta \right) \\\ & \Rightarrow y=\dfrac{x}{\sqrt{2}\sin \theta }-\dfrac{\sqrt{2}\cos \theta }{\sin \theta } \\\ & \Rightarrow y=\dfrac{x}{\sqrt{2}\sin \theta }-\sqrt{2}\cot \theta \\\ \end{aligned}$
Now, this line will cut the x axis at a point where y coordinate is 0 and we have been given that this point is P (h, 0), so we get,
$\begin{aligned} & \Rightarrow 0=\dfrac{h}{\sqrt{2}\sin \theta }-\sqrt{2}\cot \theta \\\ & \Rightarrow h=2\cos \theta .........\left( i \right) \\\ \end{aligned}$
Also, it will cut the y axis at a point where x coordinate is 0 and we have been given that this point is Q (0, k), so we get,

& \Rightarrow k=0-\sqrt{2}\cot \theta \\\ & \Rightarrow k=-\sqrt{2}\cot \theta \\\ & \Rightarrow k=\dfrac{-\sqrt{2}\cos \theta }{\sin \theta }..............\left( ii \right) \\\ \end{aligned}$$ On squaring equation (i) we get, $\Rightarrow {{h}^{2}}=4{{\cos }^{2}}\theta .............\left( iii \right)$ Similarly on squaring equation (ii) and using the identity ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$ we get, $$\begin{aligned} & \Rightarrow {{k}^{2}}=\dfrac{2{{\cos }^{2}}\theta }{{{\sin }^{2}}\theta } \\\ & \Rightarrow {{k}^{2}}=\dfrac{2{{\cos }^{2}}\theta }{1-{{\cos }^{2}}\theta } \\\ \end{aligned}$$ Substituting the value of the cosine function from equation (iii) in equation (iv) we get, $$\begin{aligned} & \Rightarrow {{k}^{2}}=\dfrac{2{{\cos }^{2}}\theta }{{{\sin }^{2}}\theta } \\\ & \Rightarrow {{k}^{2}}=\dfrac{2\times \dfrac{{{h}^{2}}}{4}}{1-\dfrac{{{h}^{2}}}{4}} \\\ & \Rightarrow {{k}^{2}}=\dfrac{2\times {{h}^{2}}}{4-{{h}^{2}}} \\\ \end{aligned}$$ Taking reciprocal both the sides and simplifying we get, $$\begin{aligned} & \Rightarrow \dfrac{1}{{{k}^{2}}}=\dfrac{4-{{h}^{2}}}{2\times {{h}^{2}}} \\\ & \Rightarrow \dfrac{2}{{{k}^{2}}}=\dfrac{4}{{{h}^{2}}}-1 \\\ & \Rightarrow \dfrac{4}{{{h}^{2}}}-\dfrac{2}{{{k}^{2}}}=1 \\\ \end{aligned}$$ Replacing h with x and k with y we get, $$\Rightarrow \dfrac{4}{{{x}^{2}}}-\dfrac{2}{{{y}^{2}}}=1$$ **So, the correct answer is “Option (b)”.** **Note:** Remember that always assume the unknown point on the curves like parabola, hyperbola, circle and ellipse in parametric form otherwise if you will assume it as any general variables represented by some alphabets then the calculation may become hard sometimes. Locus of a point is also known as the path traced by the point and it is the relation between x and y coordinate in a Cartesian plane that is why it is necessary to replace h with x and k with y in the end.