Question
Question: A tangent drawn to the curve \(y = f\left( x \right)\) at \(p\left( {x,y} \right)\) cuts the \(x - a...
A tangent drawn to the curve y=f(x) at p(x,y) cuts the x−axis and y−axis at A and B respectively such that BP : AP = 3 : 1 given that f(1)=1, then;
(1) Equation of the curve is x(dxdy)−3y=0
(2) Normal at (1,1) is x+3y=4
(3) Curve passes through (2,81)
(4) Equation of the curve is x(dxdy)+3y=0
(5) 3 and 4
Solution
To solve this question, we will first calculate the equation of the tangent using the general point slope form and then we will simplify the equation to calculate the x1 coordinate of x−axis . By using the section formula we will calculate the value of x coordinate of point P , then by using these two known coordinates we will calculate the equation of the tangent. Let us discuss section formula for internal division of a line, if the point P divides the line segment in the ratio m : n , then the coordinates of P(x,y) are calculated as ; P(x,y)=[m + nmx2+nx1,m + nmy2+ny1] .
Complete step-by-step solution:
The graphical representation for the given question is shown in the figure 1 , given below;
According to the given question, we have to find out equation of the tangent first;
We know the equation of a line passing thorough a point is given by;
⇒(Y−y)=dxdy(X−x) ......(1)
We can solve the above equation by considering either of the two points i.e. (x1,0) or (0,y1) .
Let us consider the x−axis co-ordinates (x1,0) , then by equation (1) , we get;
⇒(0−y)=dxdy(x1−x)
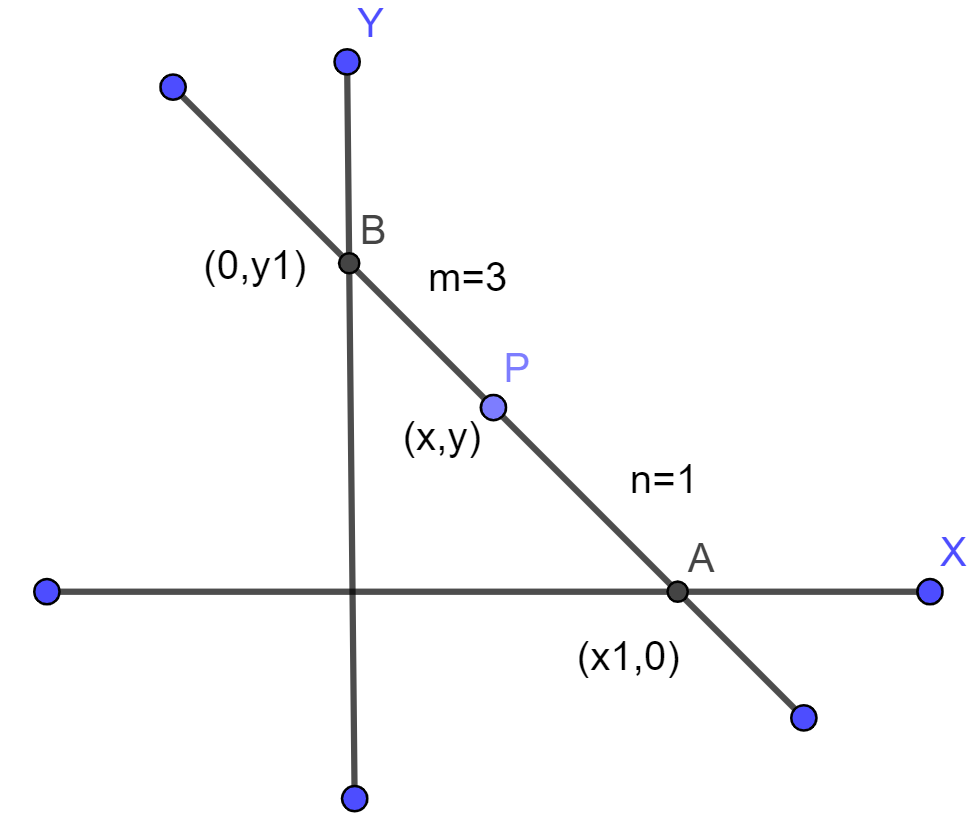
Figure $1$ : Graphical representation
Further simplifying the above equation we get;
⇒−y=dxdy(x1−x)
From the above equation we can write the value of x1 as;
⇒x1=x−ydydx ......(2)
According to the given question the tangent at point p(x,y) cuts the x−axis and y−axis at A and B and divides the line segment in the ratio 3:1 means BP : AP = 3 : 1 . So, by section formula, we can find out the value of co-ordinates of point P(x,y) .
By section formula for internal division, we know;
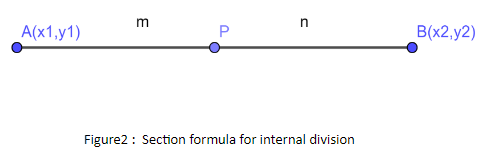
⇒(x,y)=(m+nmx2+nx1,m+nmy2+ny1)
Therefore, we can calculate the x co-ordinate of P(according to the figure 1 ) as;
⇒x=m+nmx1+nx2
⇒x=43x1+1×0
⇒x=43x1
Put the value of x1 in the above equation from equation (2) and rearranging the above equation;⇒4x=3(x−ydydx )
⇒4x=3x−3ydydx
Solving the above equation to get the equation of tangent;
⇒x=−3ydydx
⇒xdxdy=−3y
Rearranging the above equation;
⇒xdxdy+3y=0 ......(3)
Therefore, the equation of the curve is x(dxdy)+3y=0 .
Therefore , option (4) is correct.
Let us solve equation (3) further, take the x and y terms to the R.H.S. and L.H.S respectively;
⇒ydy=−3xdx
Integrating the above equation;
⇒∫ydy=−3∫xdx
(∵∫x1=logx)
⇒lny=−3lnx+lnC
By the logarithmic formula; logamn=nlogam
⇒lny=lnx−3+lnC
Again by the Property of logarithm, loga(m,n)=logam + logan
⇒lny=lnx−3C
Simplifying the above equation;
⇒y=x3C
Since it is given in the question that f(1)=1 means if input x=1 then we get the value of y=1 ;
Put the value of x=1 and y = 1 in the above equation to get the value of C ;
⇒1=1C
Therefore the value of C is;
⇒C=1
Therefore, we get the final equation as;
⇒y=x31
To check the curve passes through which point;
Put x=2 , we get the value of y as;
⇒y=81
Therefore, option (3) is also correct.
So, the answer for this question is option (5) i.e. option (3) and (4) both are correct.
Note: Since we know the equation of the tangent, we can also calculate the equation of the normal (The normal to the curve is the line perpendicular to the tangent) to the curve at that point. Since the tangent and normal are perpendicular to each other, the relationship between their slopes is given by; m1m2=−1 , where m1 and m2 are the slopes of the tangent line and normal line respectively. The slope of tangent (m1) at x = 1 and y = 1 is , dxdy(1,1)=−3 . By the relation we can calculate the slope of the normal (m2) as (−3)×m2=−1 . Therefore m2=31 . Now we can write the equation of the normal using the point slope form at x = 1 and y = 1 like y−1=31(x−1) and by further simplification, we get the equation of normal at (1,1) as x−3y+2=0 .
