Question

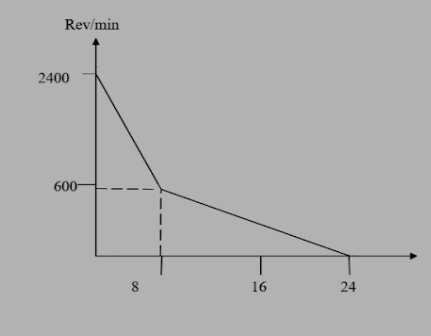
A table fan, rotating at a speed of $2400rpm$ , is switched off and the resulting variation of the rpm with time is shown in figure. The total number of revolutions of the fan before it comes to rest is.

(A) 420
(B) 280
(C) 480
(D) 380

Answer 1

A motion graph can give us the integral of the value on the Y-axis with respect to the value of X-axis by finding the slope. Also it can give us the derivative of the value on the Y-axis with respect to the value of X-axis by finding its area. For example the slope of a $V - t$ graph which shows velocity on the Y-axis and time on the X-axis, gives us the acceleration when we calculate the slope of the graph and also gives us the distance travelled when we calculate the area covered by the graph.

Formulas used : We will be using the formula to the find the area of a triangle which is $A = \dfrac{1}{2} \times b \times h$ where $A$ is the area of a triangle, $b$ is the length of the base of the triangle, and $h$ is the length of the vertical height of the triangle.
We will also be using a formula to calculate the area of a rectangle which is $A = l \times b$ where $l$ is the length of the longest side of the rectangle and $b$ is the breadth of the triangle or the length of the shortest side of the triangle.

Complete Step by Step Solution
Here we know that the fan has been rotating at an angular velocity of $\omega = 2400rev/\min$ . Referring from the graph the angular speed of the fan gradually decreases until it attains a state of complete rest at time, $t = 24s$
To find the distance it travels until it stops, is the angular distance it travelled given by, $\omega = \dfrac{{d\theta }}{{dt}}$ which can be found from the graph by finding the area covered by it. The area the graph covers appears to be composed of two triangles and a rectangle. Thus the area of the region covered by the graph is given by,
$A = \dfrac{1}{2} \times \dfrac{8}{{60}} \times 2400 + \dfrac{1}{2} \times \dfrac{{(24 - 8)}}{{60}} \times 600 + 600 \times \dfrac{8}{{60}}$
(The corresponding values of the time axis have been divided by 60 to give the value in minutes.)
Solving for $A$ we get,
$A = 120 + 80 + 80 = 280rev$
Thus the distance the fan rotates before coming to complete rest is $A = 280rev$ .
Hence the correct answer is option B.

Note
If we want to cross-check our solution we can always check using the formula $\theta = \omega t$ . For each interval the course of the graph changes from a uniform velocity.