Question

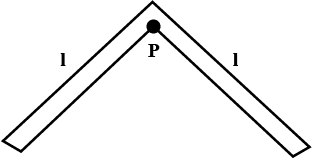
A system of two identical rods (L-shaped) of mass $m$ and length $l$ are resting on a peg $P$ as shown in the figure. IF the system is displaced in its plane by a small angle $\theta$, find the period of oscillations:

A.$2\pi \sqrt {\dfrac{{\sqrt {2l} }}{{3g}}}$
B.$2\pi \sqrt {\dfrac{{2\sqrt 2 l}}{{3g}}}$
C.$2\pi \sqrt {\dfrac{{2l}}{{3g}}}$
D.$3\pi \sqrt {\dfrac{l}{{3g}}}$

Answer 1

A pendulum is said to be consisting of an object that is suspended along an axis that is free to move back and forth easily. There are two types of pendulum one is a simple pendulum and the other is a compound pendulum. The compound pendulum is also called the physical pendulum. It is a rigid body that is pivoted so that it can oscillate freely. The given pendulum in the question is the compound pendulum.

Complete answer:
Given that there are two identical rods each of length $l$ that is resting on a peg $P$ . Given that we have to find the period of oscillations. A compound pendulum is usually a point known as the center of oscillation.
The formula for the time period of the compound pendulum is given by,
$T = 2\pi \sqrt {\dfrac{{{I_{support}}}}{{mg{l_{cm}}}}}$ …….. (1)
Here, ${I_{support}}$ is the moment of inertia of rods about the supporting point. Since there are two rods we need to multiply this term by $2$. Also, the moment of inertia of the rod when the axis of the rod goes through the end of the rod is given as
${I_{support}} = 2 \times {I_{support}} = 2 \times \dfrac{{m{l^2}}}{3}$
Also, ${l_{cm}}$ is the distance of the rod from the center of mass.
Since both, the rods are inclined by ${90^0}$
${l_{cm}} = \cos {45^0} = \dfrac{1}{{\sqrt 2 }}$
Therefore substituting all these in the equation (1) we get,
$T = 2\pi \sqrt {\dfrac{{2 \times \dfrac{{m{l^2}}}{3}}}{{mg\dfrac{1}{{\sqrt 2 }}}}}$
Solving the above equation we get,
$T = 2\pi \sqrt {\dfrac{{2\sqrt 2 l}}{{3g}}}$

Therefore the correct option is (B).

Note:
The simple pendulum’s time period and therefore its frequency depends only on the length of the string and the acceleration due to gravity. The time period of the simple pendulum reduces to $T = 2\pi \sqrt {\dfrac{l}{g}}$ . Whereas the compound pendulum’s time period and therefore its frequency depends on the length of the gyration, the mass of the pendulum, the moment of inertia, and the acceleration due to gravity.