Question
Question: A system of two blocks A and B are connected by an inextensible massless string as shown in figure. ...
A system of two blocks A and B are connected by an inextensible massless string as shown in figure. The pulley is massless and frictionless. Initially, the system is at rest. A bullet of mass ‘m’ moving with a velocity ‘u’ as shown hits block ‘B’ and gets embedded into it. The impulse imparted by tension force to the block of mass 3m is
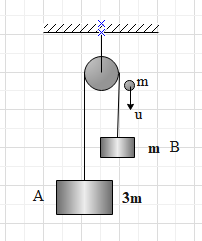
A. 45muB. 54muC. 52muD. 53mu
Solution
As there is no external force on the system, we can use the conservation of momentum on the system. Again, the change in momentum of the system will be the final momentum of block B. the momentum of block A can be found out as the impulse on the system. Equating the above two expressions, we can find the required answer.
Complete answer:
Let, the velocity of the two blocks after the collision of the bullet with the block B is v.
The mass of the block A is 3m, the mass of block B is m and the mass of the bullet is m.
The bullet is moving with a velocity u before the collision.
Let the tension on the string on the pulley at the time of the collision is T.
Impulse provided b7 the tension will be, I=∫Tdt
After the collision of the bullet with block B, the mass of the block B will be m+m=2m
Change in momentum of the bullet will be,
mu−I=2mvmu−∫Tdt=2mv∫Tdt=mu−2mv
Again, the change in momentum of the block A will be,
∫Tdt=3mv
Comparing the above two equations we can write,
mu−2mv=3mvmu=5mvv=5u
So, the impulse provided by the tension force to the block of mass 3m will be,
I=∫Tdt=3mvI=3m5uI=53mu
So, the correct answer is “Option D”.
Note:
Impulse of an object can be defined as the change in momentum of an object when a force acts on the body over a certain interval of time. It can be mathematically expressed as the force acting on the object multiplied by the time interval.
I=F×Δt
