Question
Question: A system of three charges is placed as shown in the figure: if D>>d the potential energy of the syst...
A system of three charges is placed as shown in the figure: if D>>d the potential energy of the system is best given by.
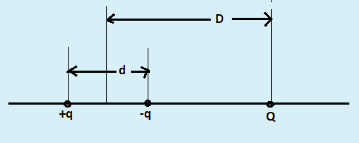
(A). 4π∈o1[+dq2+D22qQd]
(B). 4π∈o1[−dq2+2D2qQd]
(C). 4π∈o1[−dq2−D2qQd]
(D). 4π∈o1[−dq2−2D2qQd]
Solution
Hint: First we write the formula for potential energy that is UE(r)=4π∈o1[rQq]. Then find the potential energy for bringing each point charge in the presence of other charges. After that Add all the potential energy that is UQ(r)+U−qQ(D−2d)+U+q−q(d)+U+qQ(D+2d) to find the total potential energy of the system.
Formula used - UE(r)=4π∈o1[rQq].
Complete step-by-step solution -
The electric potential energy of a system of point charges is defined as the work required assembling this system of charges by bringing them close together, from an infinite distance. The SI unit of electric potential energy is the joule.
Let us assume the potential energy of a point charge after bringing it from an infinite distance in the presence of another point charge. And the distance between them is r. So using this above definition we get
UE(r)=4π∈o1[rQq] --------------------------------------- (1)
Now using equation (1) and the figure provided in the question, first finding the potential energy in bringing the first point charge from infinity. Here as no other charge is present the potential energy will be zero as shown in figure 1.
__
Figure 1
UQ(r)=4π∈o1[rQ×0]=0------------------------------------- (2)
Now the potential energy in bringing point charge −q from infinity to a point which is D−2d distance from charge Q as shown in figure 2.
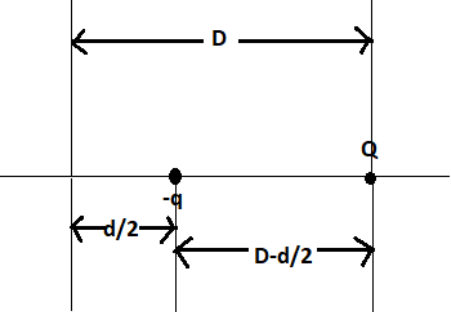
Figure 2
U−qQ(D−2d)=4π∈o1D−2dQ×(−q)=4π∈o1[2D−d−2Qq]------------------ (3)
Now the potential energy in bringing a point charge +q from infinity to a point which is D+2d distance from Q and d distance from point charge −q as shown in figure 3
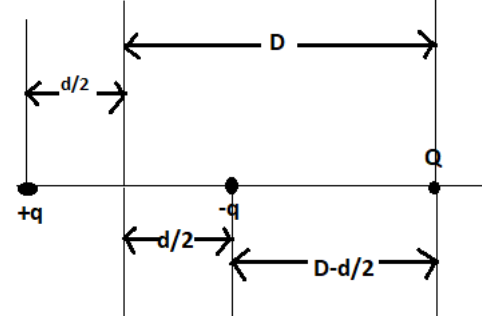
Figure 3
U+q−q(d)+U+qQ(D+2d)=4π∈o1[d(+q)×(−q)]+4π∈o1D+2dQ×(+q)
=4π∈o1([d(+q)×(−q)]+[2D+d2Q×(+q)])
=4π∈o1(d−q2+2D+d2Qq)=4π∈oq(d−q+2D+d2Q)
Taking LCM we get
U+q−q(d)+U+qQ(D)=4π∈oq(d(2D+d)−q2D−qd+2Qd)-------------------------- (4)
For the total potential energy add equation (2), (3), and (4)
UQ(r)+U−qQ(D−2d)+U+q−q(d)+U+qQ(D+2d)=0+4π∈o1[2D−d−2Qq]+4π∈oq(d(2D+d)−q2D−qd+2Qd)
Taking LCM, we get
=4π∈oq(d(2D+d)−q2D−qd+2Qd+2D−d−2Q)=4π∈oq(d(4D2−d2)−4qD2+2qdD−2qdD+qd2+4DQd−2Qd2−4DQd−2Qd2)
=4π∈oq(d(4D2−d2)−4qD2+qd2−4Qd2)=4π∈oq(d(4D2−d2)−q(4D2−d2)−4Qd2)=4π∈oq(d−q−4D2−d24Qd)
As D≫d we can write 4D2−d2≈4D2
Hence UQ(r)+U−qQ(D−2d)+U+q−q(d)+U+qQ(D+2d)=−4π∈o1(dq2+D2qQd)
So option C is correct.
Note: For these types of questions first, recall the formula for potential energy and find individual potential energy for each charge in the presence of other charges. Take care of the sign convention. As potential energy is a scalar quantity we can simply add the individual potential energy to find the total potential energy of the system.
