Question

A system of identical cylinders and plates is shown in figure. All the cylinders are identical and there is no slipping at any contact. The velocity of lower and the upper plates are v and 2v respectively, as shown. Then the ratio of angular speeds of the upper cylinder to lower cylinder is :

A. $\dfrac{1}{3}$
B. 3
C. 1
D. none of these

Answer 1

In order to solve this question we can consider any one cylinder from the upper pair and one cylinder from the lower pair. By calculating the net velocity at two points in one cylinder and solving two equations we can find the angular velocity of the upper cylinder. The net velocity of the point in contact with the plate will be the same as the velocity of the plate. Similarly consider two points in the lower cylinder and find angular velocity .Then divide both the angular velocities to find the final answer.

Complete step-by-step solution:
It is given that the velocity of the lower plate is v and the velocity of the upper plate is 2v .
We need to find the ratio of angular speeds of the upper cylinder to lower cylinder shown in the figure.
For this we can consider any one cylinder from the upper pair and one cylinder from the lower pair.
Suppose the linear velocity of the upper cylinder be denoted as $v'$ and its angular velocity be $\omega '$ .
Let us consider two diametrically opposite points P and Q.

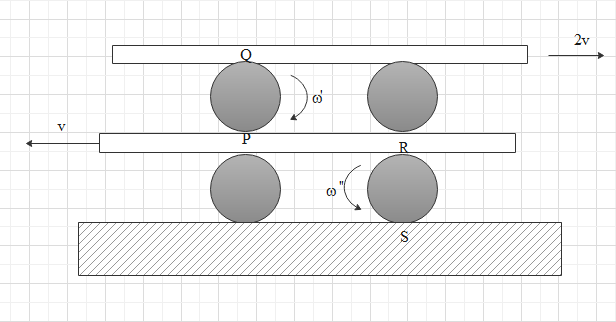
The point P is in contact with the lower plate .
The angular velocity is related to linear velocity as $\omega = \dfrac{v}{R}$
Using this the angular velocity $\omega '$ of the upper cylinder is related to $v'$ as $\omega ' = \dfrac{{v'}}{R}$
The net velocity at point P can be written as
$\overrightarrow {{v_P}} = - \omega 'R + v'$
Since at point P velocity $v'$ is towards right and $\omega 'R$ is towards left we took negative sign for $\omega 'R$.
We know that the net velocity P will be the velocity of the plate v since it is in contact with the plate.
Thus ,
$v = - \omega 'R + v'$ (1)
Now for point Q we can write the bet velocity as
$\overrightarrow {{v_Q}} = \omega 'R + v'$
Since point Q is in contact with the upper plate its net velocity will be 2v.
Thus ,
$2v = \omega 'R + v'$ (2)
On solving 1 and 2 we get
$2\omega 'R = 3v$
$\Rightarrow \omega ' = \dfrac{{3v}}{{2R}}$
Now let us consider a cylinder from the lower pair .
Consider two pints R and S . R is in contact with the lower plate and S is in contact with the ground.
Let the linear velocity of this cylinder be $v''$ and its angular velocity be $\omega ''$ in the anticlockwise direction.
Net velocity at point R can be written as
$\overrightarrow {{v_R}} = v'' + \omega ''R$
This velocity is equal to the velocity of plate v. thus we can write
$v = v'' + \omega ''R$ (3)
For point S we can write net velocity as
$\overrightarrow {{v_S}} = \omega ''R - v''$
Since it is in contact with ground velocity is zero at this point .
Thus we can write
$0 = \omega ''R - v''$ (4)
On solving equation 3 and 4 we get ,
$v = 2\omega ''R$
$\Rightarrow \omega '' = \dfrac{v}{{2R}}$
Now let us divide $\omega '$ with $\omega ''$ . then we get ,
$\dfrac{{\omega '}}{{\omega ''}} = \dfrac{{\dfrac{{3v}}{{2R}}}}{{\dfrac{v}{{2R}}}}$
$\therefore \dfrac{{\omega '}}{{\omega ''}} = 3$
So the correct answer is option B.

Note:- While calculating the net velocity at points take care of the direction of linear velocity and angular velocity. In the case of the upper cylinder at point Q the direction of angular velocity and linear velocity is the same since the rotation is taken clockwise. But at point P the direction is opposite to each other so we have to take minus signs there. Similarly in the case of the lower cylinder the rotation is anticlockwise and the direction of angular velocity and linear velocity is same at point R but opposite to each other at point S.