Question
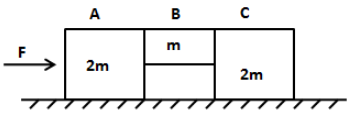
Question: A system is pushed by a force \(F\)as shown in figure all the surfaces are smooth except between \(B...
A system is pushed by a force Fas shown in figure all the surfaces are smooth except between B and C. Frictional coefficient between B and C is μ. Minimum value of F to prevent block B from downward slipping is
Solution
In order to deal with this question we have to keep in mind that Bwill not slide shown down if the frictional force is more than the weight of blockB, so we will find the normal force. The frictional force is the product of the normal force and the coefficient of friction.
Complete step by step answer:
We have given that there are three bodies having masses in the order 2m, m and 2m respectively. Then horizontal acceleration of the system is,
a=MF
Here, F is the applied force and M is the total mass of the blocks.
a=2m+m+2mF
⇒a=5mF
Now we will the calculate the normal force between Aand Bwhich will be calculated as,
N=M×a
⇒N=2m×5mF
⇒N=52F
As we know that the frictional force is given by the product of frictional coefficient and the normal force. As for this case we know the frictional coefficient and the normal force so the frictional force is given as:
Frictional force=frictional coefficient ×normal force.
⇒Ff=μ×N
⇒Ff=μ×52F
From the figure it has been cleared that Bwill not slide down if frictional force is more than the weight of block B.
So, the minimum value of F to prevent block B from down ward slipping is given the inequality.
Ff⩾W
⇒μ52F⩾Mg
∴F⩾2μ5mg
Hence the minimum value of F to prevent block B from down word slipping is 2μ5mg.
Note: Frictional force refers to the force generated by two surfaces that contact and slide against each other. Thus, forces are mainly influenced by the structure of the surface and the amount of force which needs them together. In the solution, note that the frictional force is directed upwards while the weight of the body is always downwards.
