Question

A system consists of two identical cubes each of mass m linked together by a masses spring of spring constant k. The spring is compressed by x connecting cubes by thread. Find the minimum value of x for which the lower cube will bounce up after the thread has been burnt.

& A)\dfrac{2mg}{k} \\\ & B)\dfrac{3mg}{k} \\\ & C)\dfrac{3mg}{2k} \\\ & D)\dfrac{mg}{2k} \\\ \end{aligned}$$

Answer 1

When spring is compressed/extend then interatomic forces come into play which opposes the change .So work has to be done against restoring forces and this work gets stored in the spring as elastic potential energy. When spring is compressed or released then restoring force is directly proportional to opposite of displacement.

Complete answer:
Initially both the cubes of mass m are connected by massless spring of spring constant k and a thread is also connected between the two masses.

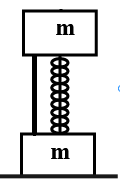
This lower block will bounce up only when there is an extension in the spring because due to extension force acts in upwards direction if there is compression then force acts in downwards direction then lower block will not be able to move upwards.
Draw Free body diagram of lower block as shown figure:-

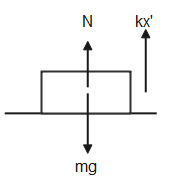
Its weight $mg$acts vertically downwards and Normal reaction due to surface is N acts perpendicular to surface and force of extension on spring due to lower block is $k{{x}^{'}}$acts vertically upwards.
Lower block will bounce up only when normal reaction$N=0$.
So, the elongation produced be ${{x}^{'}}$ such that$k{{x}^{'}}=mg$.
Simplifying it we get
{{x}^{'}}=\dfrac{mg}{k}$$$$(Equation1)
Upper block velocity gets zero when it can attain maximum displacement.
Apply conservation of energy,
(Since Kinetic Energy is zero so only Elastic potential energy exists).
Initial Elastic potential energy = Final Elastic potential energy.
So we get,
$\dfrac{1}{2}k{{x}^{2}}=mg(x+{{x}^{'}})+\dfrac{1}{2}k{{x}^{'}}^{2}$
$\Rightarrow k{{x}^{2}}=2mgx+2mg{{x}^{'}}+k{{x}^{'}}^{2}$
Putting the value of ${{x}^{'}}$from equation 1 in above equation
$\Rightarrow k{{x}^{2}}=2mgx+2mg(\dfrac{mg}{k})+k{{(\dfrac{mg}{k})}^{2}}$
$\Rightarrow k{{x}^{2}}=2mgx+\dfrac{3{{m}^{2}}{{g}^{2}}}{k}$
$\Rightarrow {{k}^{2}}{{x}^{2}}-2mgkx-3{{m}^{2}}{{g}^{2}}=0$
This is the required quadratic equation in x. On solving this we can find the value of x
${{k}^{2}}{{x}^{2}}-3mgkx+mgkx-3{{m}^{2}}{{g}^{2}}=0$
$\Rightarrow kx(kx-3mg)+mg(kx-3mg)=0$
$\Rightarrow (kx-3mg)(kx+mg)=0$
Multiplying of these two brackets is zero. So either the first bracket will be zero or the other bracket is zero.
Now when first bracket tends to zero, we get
$\Rightarrow (kx-3mg)=0$
$\therefore x=\dfrac{3mg}{k}$
When second bracket tends to zero, we get
$\Rightarrow (kx+mg)=0$
$\therefore x=\dfrac{-mg}{k}$.
This negative value of x is not possible. So this value is not valid.
So minimum value of x is $\dfrac{3mg}{k}$

Correct Option is B.

Note:
In the given question it is mentioned that the lower block will bounce up which can be done only when force on the lower block will act in upward direction and this force is provided by spring when it is extended upwards as thread is burnt then upper block will move in upwards direction till its velocity becomes zero.