Question

A system consists of three identical masses m1​, m2​ and m3​ connected by a string passing over a pulley P. The mass m1​ hangs freely and m2​ and m3​ are on a rough horizontal table (the coefficient of friction $= \mu$). The pulley is frictionless and of negligible mass. The downward acceleration of mass m1​ is:

Answer 1

This given problem can be solved by taking the consideration of motion of bodies on a frictional surface and under the gravitational force when these bodies are connected with each other by a string and hanged on some light and frictionless pulley.

Step-by-step solution:
Step 1: As given in the question three identical masses $\mathop m\nolimits_1$​, $\mathop m\nolimits_2$​ and $\mathop m\nolimits_3$​ connected by a string passing over a pulley P. The mass $\mathop m\nolimits_1$​ is hanging freely and other two masses $\mathop m\nolimits_2$​ and $\mathop m\nolimits_3$ are kept at the surface and the frictional coefficient of this surface is $\mu$.

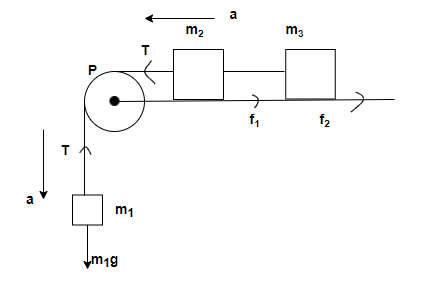
Let us consider that the mass $\mathop m\nolimits_1$ moves downward with acceleration $a$. So, the masses $\mathop m\nolimits_2$​and $\mathop m\nolimits_3$also move on horizontal surface with acceleration $a$.
The given pulley is light in weight and frictionless so tension $T$ in the string will be the same at each n every point.
As shown in the above figure forces should be balanced out for the closed system.
Step 2: So, for the motion of horizontal blocks –
$\left( {\mathop m\nolimits_2 + \mathop m\nolimits_3 } \right)a = T - \mathop f\nolimits_1 - \mathop f\nolimits_2$; where $\mathop f\nolimits_1$ is frictional force on mass $\mathop m\nolimits_2$, $\mathop f\nolimits_2$ is frictional force on mass $\mathop m\nolimits_3$, and $\left( {\mathop m\nolimits_2 + \mathop m\nolimits_3 } \right)a$ is force on masses $\mathop m\nolimits_2$​and $\mathop m\nolimits_3$ due to acceleration.
It is given that all three masses are identical so let $\mathop m\nolimits_{1 = } \mathop m\nolimits_{2 = } \mathop m\nolimits_3 = m$
And, $\mathop f\nolimits_1 = \mathop f\nolimits_2 = \mu mg$ i.e. frictional forces on masses $\mathop m\nolimits_2$​and $\mathop m\nolimits_3$.
$2ma = T - 2\mu mg$ …………………..(1)
Step 3: For the motion of vertical block –
$\mathop m\nolimits_1 a = \mathop m\nolimits_1 g - T$ or
$ma = mg - T$ ……………………………..(2)
So, from equation (1) and (2), we will get
$T = mg - ma$
$2ma = mg - ma - 2\mu mg$ on rearranging this equation, we will get –
$3ma = \left( {1 - 2\mu } \right)mg$on further solving this equation
$a = \dfrac{{\left( {1 - 2\mu } \right)g}}{3}$

So, the correct answer is $a = \dfrac{{\left( {1 - 2\mu } \right)g}}{3}$.

Note:
-It should be remembered that friction always opposes the relative motion and because of that frictional force will always be opposite to the motion due to acceleration.
-Remember that friction will be there only when the body is actually sliding/rolling over the surface of another body.