Question
Question: A symmetric star conducting wire loop is carrying a steady current \(I\) as shown in the figure. The...
A symmetric star conducting wire loop is carrying a steady current I as shown in the figure. The distance between the diametrically opposite vertices of the star is 4a. The magnitude of the magnetic field at the center of the loop is
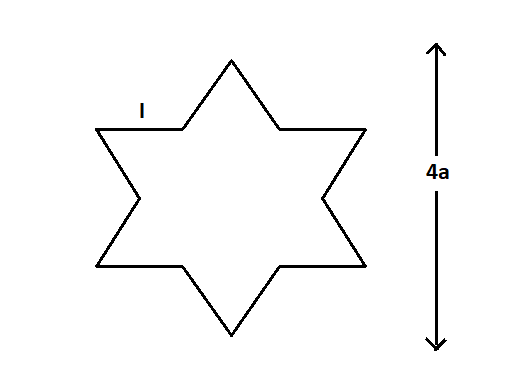
(A) 4πaμ0I6(3−1)
(B) 4πaμ0I6(3+1)
(C) 4πaμ0I3(3−1)
(D) 4πaμ0I3(2−3)
Solution
Hint We have a conductor in the shape of a symmetric star. The current I is flowing through the conductor. We know that there will be a magnetic field associated with the charges moving through a conductor. The total length between two diametrically opposite vertices of the star is given and we have to find the magnitude of the magnetic field at the center of the star.
Complete step by step answer:
According to the right-hand thumb rule, the magnetic field due to the star-shaped current-carrying conductor will be in the upward direction. Since there are 6 vertices, and each vertex has two sides the total magnetic field will be 12 times the field due to one side.
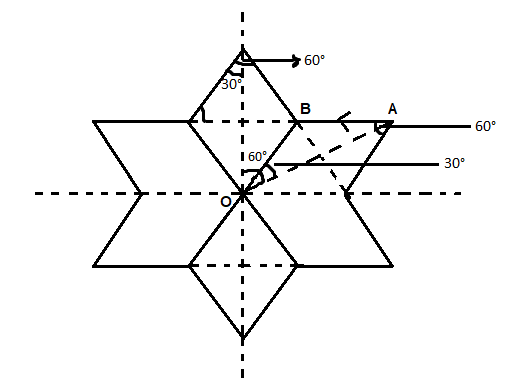
Let us consider any one of the sides as AB.
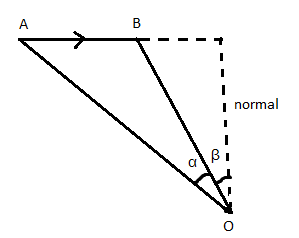
The field at a point O can be obtained by joining A and B as shown in the figure.
The dotted lines show the normal perpendicular to the point O.
The general formula for the field at the point Ocan be written as,
B=4πaμ0I(sinα−sinβ)
From the above two diagrams, we get
α=60∘ and β=30∘
Where B stands for the magnetic field, μ0 stands for the permeability of free space, I stands for the current, a stands for the distance between the conductor and the point where we have to find the electric field, and αand β are the angles as shown in the figure.
Let us assume that the field due to the side AB at the center of the star is B1.
The field B1 can be written as,
B1=4πaμ0I(sin60∘−sin30∘)
We know that sin60∘=23and sin30∘=21
Substituting the value, we get
B1=4πaμ0I(23−21)
This is the magnetic field due to one side of the star.
We know that the total magnetic field at the center of the star will be 12 times B1
Therefore, we can write the total magnetic field at the center of the star will be,
B=12×4πaμ0I(23−21)
This will be,
B=4πaμ0I6(3−1)
The answer is: Option (A): 4πaμ0I6(3−1)
Note
The strength of the magnetic field will be directly proportional to the current through the conductor. The magnetic field will also depend on the length of the conductor that we consider. It is also proportional to the sine angle between the element in the direction of current and the line joining the element and the point of consideration. The magnetic field is inversely proportional to the distance between the conductor and the point of consideration.
