Question

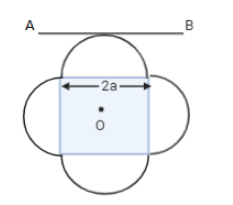
A symmetric lamina of mass M consists of a square shape with a semi-circular section over each of the edges of the square, as shown. The side of the square is 2a. The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is $1.6M{a^2}$. Calculate the moment of inertia of the lamina about the tangent AB in the plane of the lamina.

Answer 1

The moment of inertia an axis parallel to the tangent AB is calculated from the perpendicular axes theorem and then we can calculate the moment of inertia of the given lamina about the tangent AB from the parallel axes theorem.

Complete step by step answer:
A symmetric lamina whose mass is M consists of a square shape with a semi-circular section over each of the edges of a square i.e., four semi-circles are of same measures. The side of the square is 2a and the moment of inertia about an axis through its centre of mass and perpendicular to the plane is $1.6M{a^2}$ .
The theorem of perpendicular axes states that the moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moments of inertia of the lamina about any two mutually perpendicular axes in the same plane intersecting each other at the point through which the perpendicular axis passes.
Thus, Moment of inertia about an axis through its centre of mass and perpendicular to the plane (z-axis) = moment of inertia about x-axis + moment of inertia about an y-axis
$\Rightarrow 1.6M{a^2} = {I_x} + {I_y}$
$\Rightarrow 1.6M{a^2} = I + I$ [moment of inertia is same about both the axes as it is a symmetric lamina]
$\Rightarrow 1.6M{a^2} = 2I$
$\Rightarrow I = 0.8M{a^2}$
The theorem of parallel axes states that the moment of inertia of a body about any axis is equal to its moment of inertia about a parallel axis through its centre of gravity plus the product of mass of the body and the square of the perpendicular distance between the two parallel axis i.e.,
${I_{AB}} = {I_g} + M{d^2}$ where ${I_{AB}}$ is moment of inertia about the tangent AB, ${I_g}$ is the moment of inertia about its centre of gravity and d is the distance between tangent AB and parallel axis passing through its centre.
${I_{AB}} = I + M{\left( {a + a} \right)^2}$ [${I_g} = I$ and a is the radius of semi-circular region and also half of the measure of a edge of a square]
$\Rightarrow{I_{AB}} = 0.8M{a^2} + M{\left( {2a} \right)^2}$
$\Rightarrow{I_{AB}} = 0.8M{a^2} + 4M{a^2}$
$\therefore{I_{AB}} = 4.8M{a^2}$

Therefore, the moment of inertia of the lamina about the tangent AB in the plane of the lamina is $4.8M{a^2}$.

Note: The lamina in the given question is symmetric and hence the moment of inertia is the same about both the x and y axis. The diameter and side of the square both are of the same measure. Hence, the radius of the semicircular region is equal to the half of the side of the square.