Question
Question: A symmetric lamina of mass \(M\) consists of a square shape with a semi-circular section over the ed...
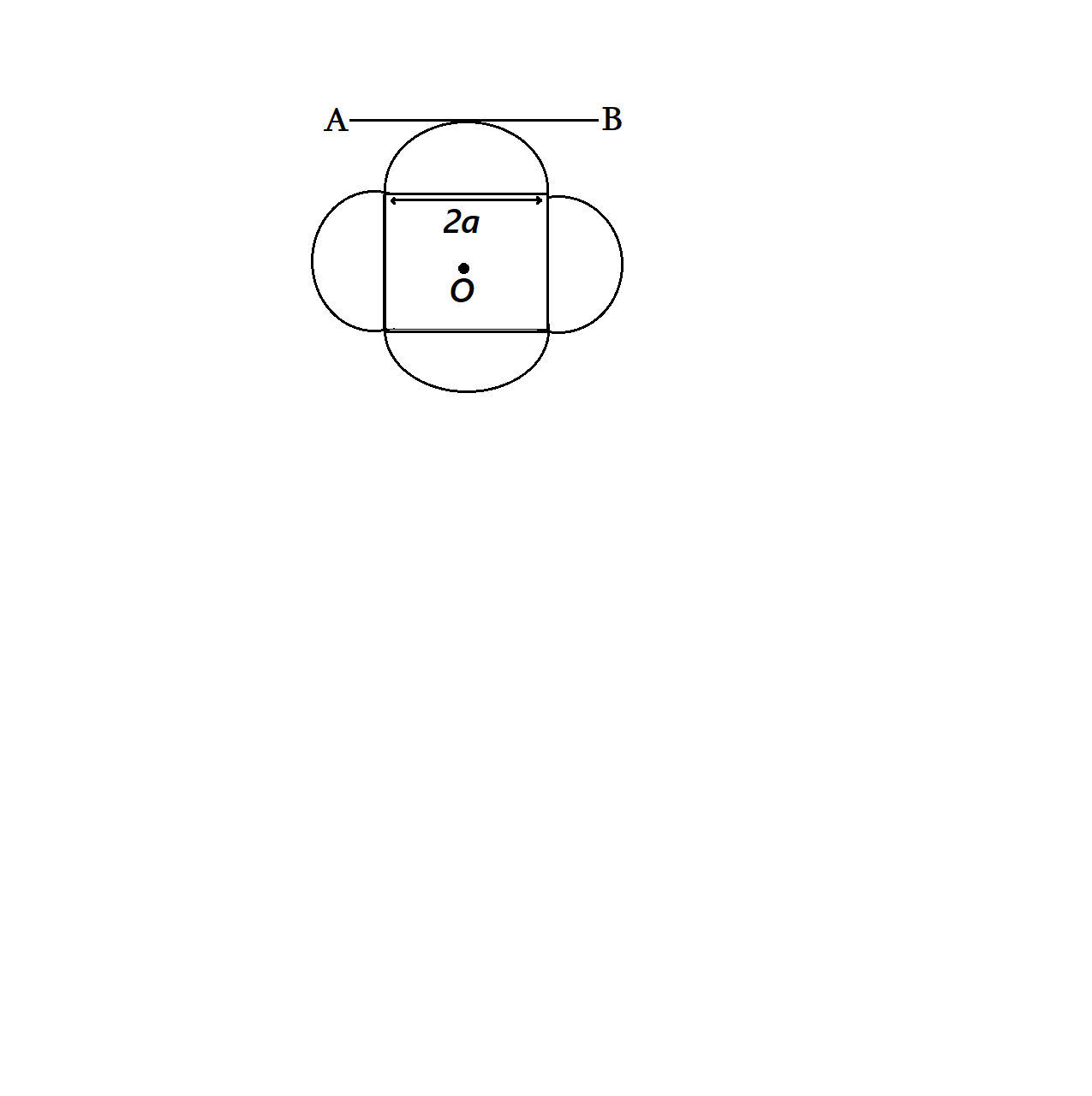
A symmetric lamina of mass M consists of a square shape with a semi-circular section over the edge of the square as shown in figure. The side of the square is 2a. The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is 1.6Ma2. The moment of inertia of the lamina about the tangent AB in the plane of the lamina is ……..
Solution
Hint: For finding the moment of inertia of the lamina about the tangent in the plane, we will use the Perpendicular axis theorem and Parallel axis theorem. For finding MOI about point O, a perpendicular axis theorem will be applied and for calculating MOI about AB, parallel axis theorem will be applied to get the required answer.
Formula used:
Perpendicular axis theorem, IZ=IX+IY
Parallel axis theorem, I=IC+Mh2
Complete step by step answer:
The moment of inertia of a lamina about an axis is a measure of how difficult it is to rotate the lamina along that axis.
Perpendicular axis theorem states that the moment of inertia of a planar lamina about an axis perpendicular to the plane of lamina is equal to the sum of the moments of inertia of the lamina about the two axes at right angles to each other at the point where the perpendicular axis passes through it.
IZ=IX+IY
Parallel axis theorem states that the value of moment of inertia of the body about an axis parallel to the body and passing through its centre is equal to the sum of moment of inertia of that same lamina or body about the axis passing through its centre and the product of mass of the body and the square of distance between two axes.
I=IC+Mh2
Using perpendicular axis theorem, we have,
IZ=IX+IY
As, IX=IY
We get, 2IX=IZ
Thus, IX=1.6Ma2
Using parallel axis theorem, we have,
IAB=IX+M(a+a)2
Therefore, IAB=4.8Ma2
The moment of inertia of the lamina about the tangent AB in the plane of the lamina is 4.8Ma2.
Note: While calculating the moment of inertia of a body, the axis should be used accordingly to find the value. A body has different values of moment of inertia about different axes. Perpendicular axis theorem and Parallel axis theorem should be used carefully choosing the appropriate axes.
