Question

A switch S is closed in the circuit shown in figure, current passed through point A is?

A. $4.5\,{\text{A}}$
B. $6.0\,{\text{A}}$
C. $3.0\,{\text{A}}$
D. Zero

Answer 1

We are given to find the value of current through point A. The resistance values of all branches are given, to find the current we need to first find the value of voltage. Use Kirchhoff’s junction rule to find the value of voltage V and then calculate the value of current passing through point A.

Complete step by step answer:
To find the current at point A, we will use Kirchhoff’s junction rule.
According to Kirchhoff’s junction rule, the sum of all the currents entering and leaving a node in a circuit is always equal to zero.
Let us name the branches for simplicity

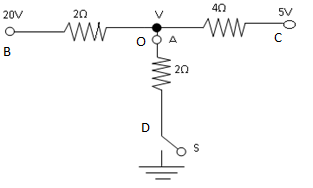
Now, we find the current through each branch
Current through branch BO is ${I_{BO}} = \dfrac{{{V_{BO}}}}{{{R_{BO}}}}$ where ${V_{BO}}$ is voltage drop across BO which is ${V_{BO}} = V - 20$ and ${R_{BO}}$ is resistance on BO branch which is given as $2{{\Omega }}$. Therefore, current through BO is ${I_{BO}} = \dfrac{{{V_{BO}}}}{{{R_{BO}}}} = \dfrac{{V - 20}}{2}$.
Current through branch CO is ${I_{CO}} = \dfrac{{{V_{CO}}}}{{{R_{CO}}}}$ where ${V_{CO}}$ is voltage drop across CO which is ${V_{CO}} = V - 5$ and ${R_{CO}}$ is resistance on CO branch which is given as ${{4\Omega }}$. Therefore, current through CO is ${I_{CO}} = \dfrac{{{V_{CO}}}}{{{R_{CO}}}} = \dfrac{{V - 5}}{4}$.
Current through branch CO is ${I_{DO}} = \dfrac{{{V_{DO}}}}{{{R_{DO}}}}$ where ${V_{DO}}$ is voltage drop across DO which is ${V_{DO}} = V - 0$ and ${R_{DO}}$ is resistance on DO branch which is given as ${{2\Omega }}$. Therefore, current through DO is ${I_{DO}} = \dfrac{{{V_{DO}}}}{{{R_{DO}}}} = \dfrac{{V - 0}}{2} = \dfrac{V}{2}$.
Now, applying Kirchhoff’s junction rule at point O we get
${I_{BO}} + {I_{CO}} + {I_{DO}} = 0$ (i)
Putting the values of ${I_{BO}}$, ${I_{CO}}$ and ${I_{DO}}$ in equation (i), we get

\Rightarrow 2\left( {V - 20} \right) + V - 5 + 2V = 0 \\\ \Rightarrow 2V + V + 2V - 40 - 5 = 0 \\\ \Rightarrow 5V = 45 \\\\$$ $$ \Rightarrow V = 9\,{\text{Volts}}$$ Now, the current through the DO branch is $${I_{DO}} = \dfrac{{V - 0}}{{{R_{DO}}}}$$. Putting the value of $$V$$ and resistance $${R_{DO}} = 2$$, we get $${I_{DO}} = \dfrac{9}{2} = 4.5\,{\text{A}}$$ **So, the correct answer is “Option A”.** **Note:** There are two Kirchhoff’s laws which are used to find the value of current and voltage of circuits. The first law is Kirchhoff’s current law or junction law which states that the sum current entering and leaving a junction of an electrical circuit is always zero. The second law or also known as voltage law states that the sum of the voltage drops around any closed circuit is always zero.