Question

A swimmer wishes to reach directly opposite the bank of a river, flowing with velocity 8 m/s. The swimmer can swim 10 m/s in still water. The width of the river is 480 m. Time taken by him to do so:
A. 60 sec
B. 48 sec
C. 80 sec
D. none.

Answer 1

At first we have to draw the diagram according to the given question to make it easier for us to solve. Now we know that as the river is flowing the man has to swim in a certain angle to reach the other bank easily. So we are finding the components of the angle that the swimmer made with the river. Then multiply the value with the velocity of the swimmer to get the actual velocity of swimming. Now, to find the time taken to cross the riven divide the total distance by the velocity of the swimmer to get the required result.
Formula used:
${{V}_{river}}={{V}_{man}}\cos \theta$
$t=\dfrac{S}{v}$

Complete answer:

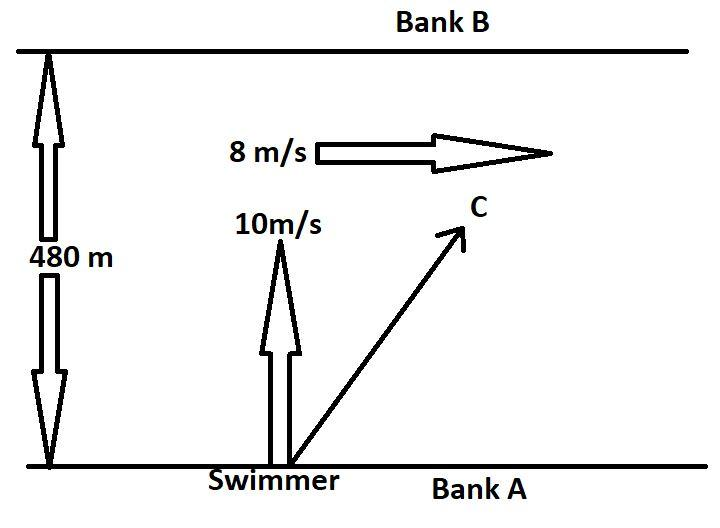
Here in the above diagram drawn according to the question, we see that the width of the river is 480 m , and there are two banks of the river Bank A and bank B respectively. The velocity of the flow of the river is 8m/s and a swimmer wants to cross the river straight from bank A to bank B and can swim at 10 m/s velocity. Now as there is velocity of the river also, the man will have to swim more as the river will push the man slowly towards the way the river is flowing and the direction that will be pursued if the man swims straight is shown in the above diagram.
Now, we know that to reach the opposite bank of the river directly the swimmer has to swim in such a way and at such an angle where the components of its velocity cancel out the velocity of flow of the river.
So if we assume that the man is swimming at an angle of $\theta$, with the flow then we get ,
${{V}_{river}}={{V}_{man}}\cos \theta$
$10\cos \theta =8$.
And also there will be another component $10\sin \theta$, which will help the swimmer to cross the river.
So, now we see that $\cos \theta =0.8$, and $\sin \theta =0.6$.
We can figure out the velocity of the man while travelling from A to B, the velocity will be,
$10\times 0.6=6m/s$ ,
And we know that the width of the river is = 480 m
So the time taken will be $t=\dfrac{S}{v}$.
$t=\dfrac{480}{6}$ ,
Which is 80 sec.

So, the correct answer is “Option C”.

Additional Information:
In the equation $t=\dfrac{S}{v}$, ‘t’ is the time taken , ‘S’ is the distance of the river and ‘v’ is the velocity of the swimmer. We must remember to find the actual velocity of the man to find the required result or else the result would not be correct.

Note:
In the equation $t=\dfrac{S}{v}$, ‘t’ is the time taken , ‘S’ is the distance of the river and ‘v’ is the velocity of the swimmer. We must remember to find the actual velocity of the man to find the required result or else the result would not be correct.